Вопрос № 874053 - Математика и информатика
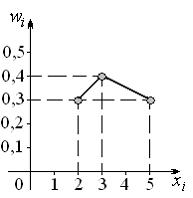
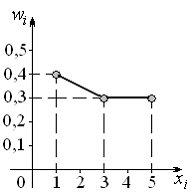
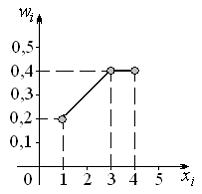
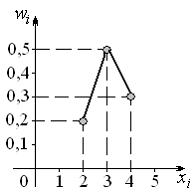
Выборочная средняя равна 3. Она соответствует выборке, представленной полигоном относительных частот …
Вопрос задал(а): Анонимный пользователь, 13 Ноябрь 2020 в 15:29
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 15:29
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 15:29
Похожие вопросы
Выборочная средняя выборки, полигон относительных частот которой задан на рисунке
равна
. Тогда выборочная дисперсия равна …
равна
. Тогда выборочная дисперсия равна …
0
2,6
1,8
2,4
Выборочная средняя выборки, полигон относительных частот которой задан на рисунке
,
равна
. Тогда выборочная дисперсия равна …
,равна
. Тогда выборочная дисперсия равна …
0
1,6
0,64
1,2
Другие вопросы по предмету Математика и информатика
Выборочная дисперсия выборки, заданной статистическим распределением 
, равна …
, равна …
4
2,6
1,8
3,2
Выборочная дисперсия выборки, заданной вариационным рядом 1, 1, 1, 2, 3, 3, 4, 4, 4, 7, равна …
3,4
0,6
3
3,2
Для оценки с некоторой надежностью 
математического ожидания 
нормально распределенного признака 
по выборочной средней 
при среднем квадратичном отклонении 
генеральной совокупности использовали доверительный интервал 
, где 
– значение аргумента функции Лапласа 
, при котором 
, 
– объем выборки.
Установите соответствие между значениями надежности
и соответствующим доверительными интервалами, если 
.
1.
2.
математического ожидания нормально распределенного признака по выборочной средней при среднем квадратичном отклонении генеральной совокупности использовали доверительный интервал , где – значение аргумента функции Лапласа , при котором , – объем выборки.Установите соответствие между значениями надежности
и соответствующим доверительными интервалами, если .1.
2.
Для оценки с надежностью 
математического ожидания 
нормально распределенного признака 
по выборочной средней 
при среднем квадратичном отклонении 
генеральной совокупности использовали доверительный интервал 
, где 
– значение аргумента функции Лапласа 
, при котором 
, 
– объем выборки. Значение аргумента функции Лапласа для 
равно 
.
Установите соответствие между объемами выборок
и соответствующим доверительными интервалами.
1.
2.
математического ожидания нормально распределенного признака по выборочной средней при среднем квадратичном отклонении генеральной совокупности использовали доверительный интервал , где – значение аргумента функции Лапласа , при котором , – объем выборки. Значение аргумента функции Лапласа для равно .Установите соответствие между объемами выборок
и соответствующим доверительными интервалами.1.
2.
