Квантовая и классическая частицы с энергией Е движущиеся слева направо встречают на своем пути потен...: ответ на тест 977501 - Физика
Квантовая и классическая частицы с энергией Е, движущиеся слева направо, встречают на своем пути потенциальный барьер высоты 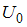 и ширины
и ширины 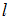 .
.
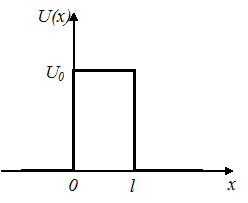
Если P − вероятность преодоления барьера, то для …
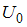 и ширины
и ширины 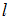 .
.
Если P − вероятность преодоления барьера, то для …
Вопрос задал(а): Анонимный пользователь, 13 Ноябрь 2020 в 16:53
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 16:53
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 16:53

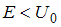
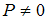 , а при
, а при 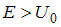
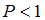
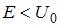
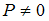 , а при
, а при 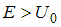
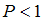
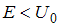
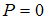 , а при
, а при 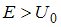
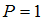
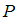 зависит только от
зависит только от 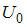 и не зависит от
и не зависит от