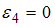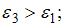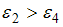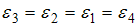Вопрос № 878678 - Физика
Диск может вращаться вокруг оси, перпендикулярной плоскости диска и проходящей через его центр. К нему прикладывают одну из сил (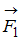
, 
, 
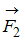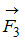или 
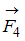), лежащих в плоскости диска и равных по модулю.
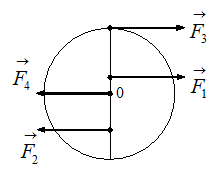
Верным для угловых ускорений диска является соотношение …
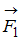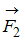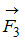, , или 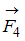), лежащих в плоскости диска и равных по модулю.Верным для угловых ускорений диска является соотношение …
, 
Вопрос задал(а): Анонимный пользователь, 13 Ноябрь 2020 в 15:32
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 15:32
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 15:32
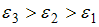Похожие вопросы
Диск может вращаться вокруг оси, перпендикулярной плоскости диска и проходящей через его центр. К нему прикладывают одну из сил (
, 
, 
или 
), лежащих в плоскости диска и равных по модулю.
Верным для угловых ускорений диска является соотношение …
, , или ), лежащих в плоскости диска и равных по модулю.Верным для угловых ускорений диска является соотношение …
, 
Диск может вращаться вокруг оси, перпендикулярной плоскости диска и проходящей через его центр. К нему прикладывают одну из сил (
, 
, 
или 
), лежащих в плоскости диска и равных по модулю.
Верным для угловых ускорений диска является соотношение …
, , или ), лежащих в плоскости диска и равных по модулю.Верным для угловых ускорений диска является соотношение …
Другие вопросы по предмету Физика
Диск вращается вокруг неподвижной оси с постоянной угловой скоростью. В некоторый момент времени на диск начинает действовать не изменяющийся со временем тормозящий момент. Зависимость момента импульса диска от времени, начиная с этого момента, представлена на рисунке линией …
B
C
A
E
D
Обруч скатывается без проскальзывания с горки высотой 2,5 м. Скорость обруча (в м/с) у основания горки при условии, что трением можно пренебречь, равна …
5
Частица совершила перемещение по некоторой траектории из точки M (3, 2) в точку N (2, –3). При этом на нее действовала сила 
(координаты точек и сила 
заданы в единицах СИ). Работа, совершенная силой 
, равна …
(координаты точек и сила заданы в единицах СИ). Работа, совершенная силой , равна …
Потенциальная энергия частицы в некотором силовом поле задана функцией 
. Работа потенциальной силы (в Дж) по перемещению частицы из точки В (1, 1, 1) в точку С (2, 2, 2) равна …
(Функция
и координаты точек заданы в единицах СИ.)
. Работа потенциальной силы (в Дж) по перемещению частицы из точки В (1, 1, 1) в точку С (2, 2, 2) равна …(Функция
и координаты точек заданы в единицах СИ.)