Вопрос № 1092060 - Физика
Задания №5, №6, №7, №8 являются составными частями одного общего II задания. Баллы заданий складываются – общий балл равен 4.
Задание №8 оценивается в 1 балл.
При решении этого задания учитывайте ответ на предшествующее задание (№7)
Если ответ на задание №7 неправильный, то ответ на задание №8 не учитывается, даже если он «угадан» верно.
Земная атмосфера нагревается в основном от контакта с земной поверхностью, поглощающей энергию солнечного излучения. Если температура воздуха достаточно быстро убывает с высотой, то нагреваемые массы воздуха будут подниматься вверх, адиабатически (показатель адиабаты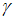
) расширяясь и охлаждаясь при этом. Это приводит к конвекции и связанному с ней нарушению механической устойчивости атмосферы.
Пусть при механическом равновесии воздуха на высотах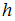
и 
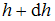(малое изменение высоты 
) над земной поверхностью его температура и давление соответственно равны 
и 
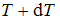(малое изменение температуры 
), 
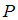и 
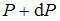(малое изменение давления 
).
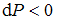Если в силу каких-либо случайных возмущений некоторая малая масса
воздуха переместилась с высоты 
на высоту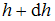 
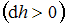, то модуль температурного градиента 
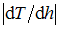(температурный градиент 
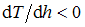) атмосферного воздуха, чтобы он мог находиться в устойчивом механическом равновесии, не должен превосходить максимальное значение, равное …
(Ответ выразите в кельвинах на километр, округлите до десятых.
Влияние влажности воздуха не учитывать. Температуру воздуха у земной поверхности принять равной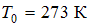
. Изменением ускорения 
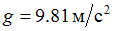свободного падения с высотой 
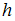над земной поверхностью можно пренебречь. Учесть, что универсальная газовая постоянная 
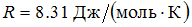, молярная масса воздуха 
.)
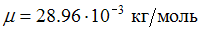Задание №8 оценивается в 1 балл.
При решении этого задания учитывайте ответ на предшествующее задание (№7)
Если ответ на задание №7 неправильный, то ответ на задание №8 не учитывается, даже если он «угадан» верно.
Земная атмосфера нагревается в основном от контакта с земной поверхностью, поглощающей энергию солнечного излучения. Если температура воздуха достаточно быстро убывает с высотой, то нагреваемые массы воздуха будут подниматься вверх, адиабатически (показатель адиабаты
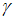) расширяясь и охлаждаясь при этом. Это приводит к конвекции и связанному с ней нарушению механической устойчивости атмосферы. Пусть при механическом равновесии воздуха на высотах
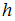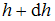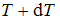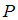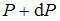и (малое изменение высоты ) над земной поверхностью его температура и давление соответственно равны и (малое изменение температуры ), и (малое изменение давления 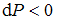).Если в силу каких-либо случайных возмущений некоторая малая масса
воздуха переместилась с высоты на высоту 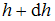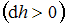, то модуль температурного градиента 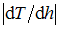(температурный градиент 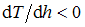) атмосферного воздуха, чтобы он мог находиться в устойчивом механическом равновесии, не должен превосходить максимальное значение, равное …(Ответ выразите в кельвинах на километр, округлите до десятых.
Влияние влажности воздуха не учитывать. Температуру воздуха у земной поверхности принять равной
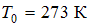. Изменением ускорения 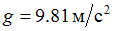свободного падения с высотой 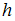над земной поверхностью можно пренебречь. Учесть, что универсальная газовая постоянная 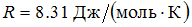, молярная масса воздуха .)
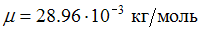Вопрос задал(а): Анонимный пользователь, 13 Ноябрь 2020 в 19:28
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 19:28
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 19:28
Похожие вопросы
Задания №5, №6, №7, №8 являются составными частями одного общего II задания. Баллы заданий складываются – общий балл равен 4.
Задание №7 оценивается в 1 балл.
При решении этого задания учитывайте ответы на предшествующие задания (№5 и №6).
Если ответ на задание №5 или №6 неправильный, то ответ на задание №7 не учитывается, даже если он «угадан» верно.
Земная атмосфера нагревается в основном от контакта с земной поверхностью, поглощающей энергию солнечного излучения. Если температура воздуха достаточно быстро убывает с высотой, то нагреваемые массы воздуха будут подниматься вверх, адиабатически (показатель адиабаты
) расширяясь и охлаждаясь при этом. Это приводит к конвекции и связанному с ней нарушению механической устойчивости атмосферы.
Пусть при механическом равновесии воздуха на высотах
и 
(малое изменение высоты 
) над земной поверхностью его температура и давление соответственно равны 
и 
(малое изменение температуры 
) и 
, 
(малое изменение давления 
).
Если в силу каких-либо случайных возмущений некоторая малая масса
воздуха переместилась с высоты 
на высоту 
, то условие механической устойчивости атмосферы имеет вид …
(Влияние влажности воздуха не учитывать. Температуру воздуха у земной поверхности принять равной
.)
Задание №7 оценивается в 1 балл.
При решении этого задания учитывайте ответы на предшествующие задания (№5 и №6).
Если ответ на задание №5 или №6 неправильный, то ответ на задание №7 не учитывается, даже если он «угадан» верно.
Земная атмосфера нагревается в основном от контакта с земной поверхностью, поглощающей энергию солнечного излучения. Если температура воздуха достаточно быстро убывает с высотой, то нагреваемые массы воздуха будут подниматься вверх, адиабатически (показатель адиабаты
) расширяясь и охлаждаясь при этом. Это приводит к конвекции и связанному с ней нарушению механической устойчивости атмосферы. Пусть при механическом равновесии воздуха на высотах
и (малое изменение высоты ) над земной поверхностью его температура и давление соответственно равны и (малое изменение температуры ) и , (малое изменение давления ).Если в силу каких-либо случайных возмущений некоторая малая масса
воздуха переместилась с высоты на высоту , то условие механической устойчивости атмосферы имеет вид … (Влияние влажности воздуха не учитывать. Температуру воздуха у земной поверхности принять равной
.) 
Задания №5, №6, №7, №8 являются составными частями одного общего II задания. Баллы заданий складываются – общий балл равен 4.
Задание №6 оценивается в 1 балл.
Земная атмосфера нагревается в основном от контакта с земной поверхностью, поглощающей энергию солнечного излучения. Если температура воздуха достаточно быстро убывает с высотой, то нагреваемые массы воздуха будут подниматься вверх, адиабатически (показатель адиабаты
) расширяясь и охлаждаясь при этом. Это приводит к конвекции и связанному с ней нарушению механической устойчивости атмосферы.
Пусть при механическом равновесии воздуха на высоте
над земной поверхностью его температура равна 
, давление – 
, плотность – 
.
Если в силу каких-либо случайных возмущений некоторая малая масса
воздуха переместилась с высоты 
на высоту 
, то при малом изменении давления 
и плотности 
, считая расширение переместившейся массы воздуха адиабатическим, плотность 
этой порции воздуха на высоте 
равна …
(Влияние влажности воздуха не учитывать. Температуру воздуха у земной поверхности принять равной
.)
Задание №6 оценивается в 1 балл.
Земная атмосфера нагревается в основном от контакта с земной поверхностью, поглощающей энергию солнечного излучения. Если температура воздуха достаточно быстро убывает с высотой, то нагреваемые массы воздуха будут подниматься вверх, адиабатически (показатель адиабаты
) расширяясь и охлаждаясь при этом. Это приводит к конвекции и связанному с ней нарушению механической устойчивости атмосферы. Пусть при механическом равновесии воздуха на высоте
над земной поверхностью его температура равна , давление – , плотность – .Если в силу каких-либо случайных возмущений некоторая малая масса
воздуха переместилась с высоты на высоту , то при малом изменении давления и плотности , считая расширение переместившейся массы воздуха адиабатическим, плотность этой порции воздуха на высоте равна … (Влияние влажности воздуха не учитывать. Температуру воздуха у земной поверхности принять равной
.) 
Другие вопросы по предмету Физика
Задания №9, №10, №11, №12 являются составными частями одного общего III задания. Баллы заданий складываются – общий балл равен 4.
Задание №9 оценивается в 1 балл.
Два цилиндрических проводника (стержня) с радиусом
и длиной 
приварены на расстоянии 
друг от друга к большому металлическому листу толщиной 
(см. рисунок). Оказалось, что удельная проводимость 
материала листа значительно меньше удельной проводимости 
проводников 
. Пусть стержни заряжены с линейной плотностью зарядов 
. Тогда напряженность поля одного стержня на расстоянии 
от его оси равна …
(Краевыми эффектами пренебречь.)
Задание №9 оценивается в 1 балл.
Два цилиндрических проводника (стержня) с радиусом
и длиной приварены на расстоянии друг от друга к большому металлическому листу толщиной (см. рисунок). Оказалось, что удельная проводимость материала листа значительно меньше удельной проводимости проводников . Пусть стержни заряжены с линейной плотностью зарядов . Тогда напряженность поля одного стержня на расстоянии от его оси равна …(Краевыми эффектами пренебречь.)
Задания №9, №10, №11, №12 являются составными частями одного общего III задания. Баллы заданий складываются – общий балл равен 4.
Задание №10 оценивается в 1 балл.
При решении этого задания учитывайте ответ на предшествующее задание (№9).
Если ответ на задание №9 неправильный, то ответ на задание №10 не учитывается, даже если он «угадан» верно.
Два цилиндрических проводника (стержня) с радиусом
и длиной 
приварены на расстоянии 
друг от друга к большому металлическому листу толщиной 
(см. рисунок). Оказалось, что удельная проводимость 
материала листа значительно меньше удельной проводимости 
проводников 
. Пусть стержни заряжены с линейной плотностью зарядов 
. Тогда разность потенциалов между стержнями равна …
(Краевыми эффектами пренебречь.)
Задание №10 оценивается в 1 балл.
При решении этого задания учитывайте ответ на предшествующее задание (№9).
Если ответ на задание №9 неправильный, то ответ на задание №10 не учитывается, даже если он «угадан» верно.
Два цилиндрических проводника (стержня) с радиусом
и длиной приварены на расстоянии друг от друга к большому металлическому листу толщиной (см. рисунок). Оказалось, что удельная проводимость материала листа значительно меньше удельной проводимости проводников . Пусть стержни заряжены с линейной плотностью зарядов . Тогда разность потенциалов между стержнями равна …(Краевыми эффектами пренебречь.)
Задания №9, №10, №11, №12 являются составными частями одного общего III задания. Баллы заданий складываются – общий балл равен 4.
Задание №11 оценивается в 1 балл.
При решении этого задания учитывайте ответ на предшествующее задание (№10).
Если ответ на задание №10 неправильный, то ответ на задание №11 не учитывается, даже если он «угадан» верно.
Два цилиндрических проводника (стержня) с радиусом
и длиной 
приварены на расстоянии 
друг от друга к большому металлическому листу толщиной 
(см. рисунок). Оказалось, что удельная проводимость 
материала листа значительно меньше удельной проводимости 
проводников 
. Пусть на стержнях поддерживаются заряды, распределенные с линейной плотностью 
. Тогда сила тока 
, вытекающего из цилиндрического проводника, равна …
(Краевыми эффектами пренебречь.)
Задание №11 оценивается в 1 балл.
При решении этого задания учитывайте ответ на предшествующее задание (№10).
Если ответ на задание №10 неправильный, то ответ на задание №11 не учитывается, даже если он «угадан» верно.
Два цилиндрических проводника (стержня) с радиусом
и длиной приварены на расстоянии друг от друга к большому металлическому листу толщиной (см. рисунок). Оказалось, что удельная проводимость материала листа значительно меньше удельной проводимости проводников . Пусть на стержнях поддерживаются заряды, распределенные с линейной плотностью . Тогда сила тока , вытекающего из цилиндрического проводника, равна …(Краевыми эффектами пренебречь.)
Задания №9, №10, №11, №12 являются составными частями одного общего III задания. Баллы заданий складываются – общий балл равен 4.
Задание №12 оценивается в 1 балл.
При решении этого задания учитывайте ответы на предшествующие задания (№10, №11).
Если ответ на задание №10 или №11 неправильный, то ответ на задание №12 не учитывается, даже если он «угадан» верно.
Два цилиндрических проводника (стержня) с радиусом
и длиной 
приварены на расстоянии 
друг от друга к большому металлическому листу толщиной 
(см. рисунок). Оказалось, что удельная проводимость 
материала листа значительно меньше удельной проводимости 
проводников 
. Тогда сопротивление 
между проводниками равно …
(Краевыми эффектами пренебречь.)
Задание №12 оценивается в 1 балл.
При решении этого задания учитывайте ответы на предшествующие задания (№10, №11).
Если ответ на задание №10 или №11 неправильный, то ответ на задание №12 не учитывается, даже если он «угадан» верно.
Два цилиндрических проводника (стержня) с радиусом
и длиной приварены на расстоянии друг от друга к большому металлическому листу толщиной (см. рисунок). Оказалось, что удельная проводимость материала листа значительно меньше удельной проводимости проводников . Тогда сопротивление между проводниками равно …(Краевыми эффектами пренебречь.)
