Даны два математических утверждения: «Через точку не лежащую на данной прямой проходит только одна п...: ответ на тест 67772 - Математика и информатика
Даны два математических утверждения: 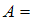 «Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной» и
«Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной» и 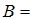 «Если две прямые параллельны третьей, то они параллельны». Тогда справедливы следующие высказывания …
«Если две прямые параллельны третьей, то они параллельны». Тогда справедливы следующие высказывания …
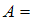 «Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной» и
«Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной» и 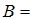 «Если две прямые параллельны третьей, то они параллельны». Тогда справедливы следующие высказывания …
«Если две прямые параллельны третьей, то они параллельны». Тогда справедливы следующие высказывания …
Вопрос задал(а): Анонимный пользователь, 18 Декабрь 2015 в 09:44
На вопрос ответил(а): Любимов Павел, 18 Декабрь 2015 в 09:45
На вопрос ответил(а): Любимов Павел, 18 Декабрь 2015 в 09:45

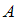 и
и 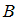 – аксиомы
– аксиомы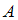 – теорема,
– теорема, 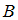 – аксиома
– аксиома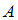 – аксиома,
– аксиома, 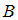 – теорема
– теорема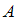 и
и 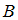 – теоремы
– теоремы