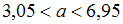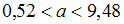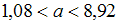Для оценки с некоторой надежностью математического ожидания нормально распределенного признака по...: ответ на тест 874056 - Математика и информатика
Для оценки с некоторой надежностью 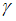 математического ожидания
математического ожидания 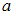 нормально распределенного признака
нормально распределенного признака 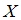 по выборочной средней
по выборочной средней 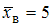 при среднем квадратичном отклонении
при среднем квадратичном отклонении 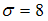 генеральной совокупности использовали доверительный интервал
генеральной совокупности использовали доверительный интервал 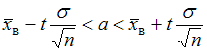 , где
, где 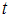 – значение аргумента функции Лапласа
– значение аргумента функции Лапласа 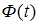 , при котором
, при котором 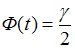 ,
, 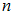 – объем выборки.
– объем выборки.
Установите соответствие между значениями надежности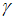 и соответствующим доверительными интервалами, если
и соответствующим доверительными интервалами, если 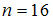 .
.
1.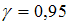
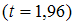
2.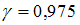
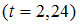
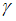 математического ожидания
математического ожидания 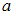 нормально распределенного признака
нормально распределенного признака 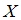 по выборочной средней
по выборочной средней 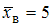 при среднем квадратичном отклонении
при среднем квадратичном отклонении 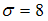 генеральной совокупности использовали доверительный интервал
генеральной совокупности использовали доверительный интервал 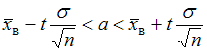 , где
, где 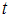 – значение аргумента функции Лапласа
– значение аргумента функции Лапласа 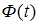 , при котором
, при котором 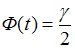 ,
, 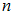 – объем выборки.
– объем выборки.Установите соответствие между значениями надежности
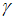 и соответствующим доверительными интервалами, если
и соответствующим доверительными интервалами, если 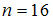 .
.1.
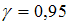
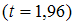
2.
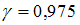
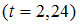
Вопрос задал(а): Анонимный пользователь, 13 Ноябрь 2020 в 15:29
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 15:29
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 15:29