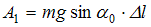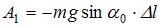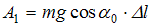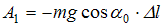Задания 1 2 3 4 являются составными частями одного общего I задания. Баллы заданий складываются общи...: ответ на тест 1080611 - Физика
Задания №1, №2, №3, №4 являются составными частями одного общего I задания. Баллы заданий складываются, общий балл равен 4.
Задание №1 оценивается в 1 балл.
Хорошо известно, что можно поддерживать колебания качелей длительное время, если быстро приседать в момент их наибольшего отклонения и также быстро вставать при прохождении положения равновесия.
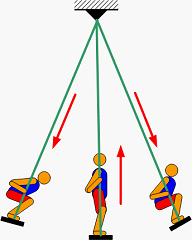
Благодаря этому параметр физического маятника (качелей) – расстояние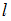 между осью вращения и центром масс – меняется быстро на величину
между осью вращения и центром масс – меняется быстро на величину 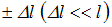 . Величина
. Величина 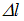 должна быть такой, чтобы компенсировать потери энергии
должна быть такой, чтобы компенсировать потери энергии 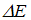 маятника за период (условие баланса энергии).
маятника за период (условие баланса энергии).
Чтобы понять, почему это так, предлагается предельно упрощенная модель человека на качелях – обычный математический маятник, то есть небольшое тело массой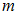 на легкой и длинной нити
на легкой и длинной нити 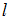 , которая меняется на величину
, которая меняется на величину 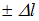 .
.
Это можно осуществить, если пропустить нить маятника через отверстие в точке P (точке подвеса) и затем, прикладывая внешнюю силу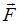 к концу нити, периодически менять ее длину.
к концу нити, периодически менять ее длину.
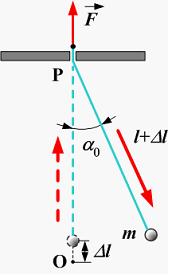
Если амплитуда установившихся колебаний маятника равна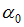 , то в момент наибольшего отклонения, быстро (мгновенно) увеличивая длину нити на величину
, то в момент наибольшего отклонения, быстро (мгновенно) увеличивая длину нити на величину 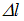 , внешняя сила
, внешняя сила 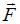 совершает работу
совершает работу 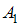 , равную …
, равную …
Задание №1 оценивается в 1 балл.
Хорошо известно, что можно поддерживать колебания качелей длительное время, если быстро приседать в момент их наибольшего отклонения и также быстро вставать при прохождении положения равновесия.

Благодаря этому параметр физического маятника (качелей) – расстояние
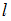 между осью вращения и центром масс – меняется быстро на величину
между осью вращения и центром масс – меняется быстро на величину 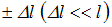 . Величина
. Величина 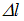 должна быть такой, чтобы компенсировать потери энергии
должна быть такой, чтобы компенсировать потери энергии 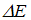 маятника за период (условие баланса энергии).
маятника за период (условие баланса энергии).Чтобы понять, почему это так, предлагается предельно упрощенная модель человека на качелях – обычный математический маятник, то есть небольшое тело массой
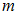 на легкой и длинной нити
на легкой и длинной нити 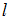 , которая меняется на величину
, которая меняется на величину 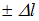 .
.Это можно осуществить, если пропустить нить маятника через отверстие в точке P (точке подвеса) и затем, прикладывая внешнюю силу
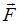 к концу нити, периодически менять ее длину.
к концу нити, периодически менять ее длину.
Если амплитуда установившихся колебаний маятника равна
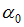 , то в момент наибольшего отклонения, быстро (мгновенно) увеличивая длину нити на величину
, то в момент наибольшего отклонения, быстро (мгновенно) увеличивая длину нити на величину 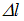 , внешняя сила
, внешняя сила 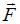 совершает работу
совершает работу 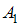 , равную …
, равную …
Вопрос задал(а): Анонимный пользователь, 13 Ноябрь 2020 в 19:24
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 19:24
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 19:24