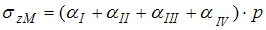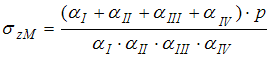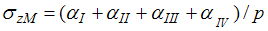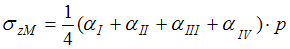Вопрос № 903917 - Механика грунтов
Вертикальное напряжение
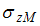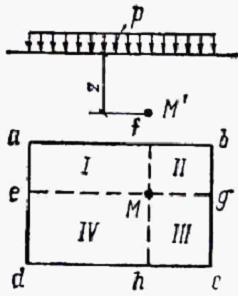
в точке М на глубине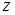 
по вертикали, проходящей внутри площадки a, f, b, g, c, h, d, e, загруженной равномерной нагрузкой 
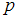, вычисляется по формуле … 
Вопрос задал(а): Анонимный пользователь, 13 Ноябрь 2020 в 16:08
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 16:08
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 16:08
Похожие вопросы
Вертикальное напряжение
в точке М на глубине 
на вертикали, проходящей через край площадки с размерами 
и 
, загруженной равномерной нагрузкой 
, где 
− природное давление на глубине 
− коэффициенты затухания напряжений для площадок, соответственно, 
, 
и 
, определяемые по СНиП 2.02.01 – 83* «Основания зданий и сооружений», вычисляется по формуле … 
=
Вертикальное напряжение
в точке М на глубине 
на вертикали, проходящей через край площадки с размерами 
и 
, загруженной равномерной нагрузкой 
, где 
− природное давление на глубине 
− коэффициенты затухания напряжений для площадок, соответственно, 
, 
и 
, определяемые по СНиП 2.02.01 – 83* «Основания зданий и сооружений», вычисляется по формуле … 
=
Другие вопросы по предмету Механика грунтов
Главные радиальные напряжения в линейно деформируемой среде от погонной нагрузки в условиях плоской задачи (см. рис.) определяются по формуле 
, предложенной …
, предложенной …
Буссинеском
Кулоном
Прандтлем
Фламаном
На рисунке показано распределение в грунте от полосовой распределенной нагрузки
изолиний напряжений …
вертикальных
горизонтальных (распоров)
от собственного веса грунта
касательных (сдвигов)
При равной величине равномерно распределенной нагрузки на площадках загружения квадратной, прямоугольной, ленточной и круглой форм наибольшие вертикальные дополнительные напряжения будут под площадкой __________ формы (глубина удаления от площадок одинакова).
круглой
прямоугольной 
квадратной 
ленточной 
Осадка разуплотнения возникает в результате …
длительной эксплуатации здания
изменения структуры грунта
замерзания и оттаивания грунта
возведения здания в открытых котлованах