На рисунке представлены графики функции распределения молекул идеального газа по скоростям распредел...: ответ на тест 926065 - Физика

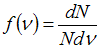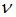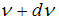На рисунке представлены графики функции распределения молекул идеального газа по скоростям (распределение Максвелла), где  – доля молекул, скорости которых заключены в интервале скоростей от  до  в расчете на единицу этого интервала.

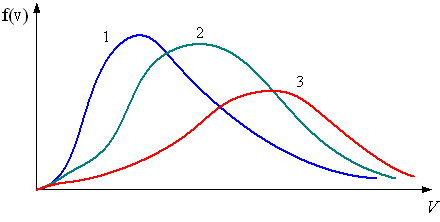
Для этих функций верными являются утверждения, что …

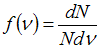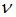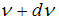На рисунке представлены графики функции распределения молекул идеального газа по скоростям (распределение Максвелла), где  – доля молекул, скорости которых заключены в интервале скоростей от  до  в расчете на единицу этого интервала.

Для этих функций верными являются утверждения, что …

Средняя кинетическая энергия молекул газа при температуре  зависит от их конфигурации и структуры, что связано с возможностью различных видов движения атомов в молекуле и самой молекулы. При условии, что имеет место поступательное, вращательное движение молекулы как целого и колебательное движение атомов в молекуле, средняя кинетическая энергия молекулы кислорода () равна …

В соответствии с законом равномерного распределения энергии по степеням свободы средняя кинетическая энергия молекулы идеального газа при температуре T равна: . Здесь , где ,  и  – число степеней свободы поступательного, вращательного и колебательного движений молекулы соответственно. Для гелия () число i равно …

При комнатной температуре отношение  молярных теплоемкостей при постоянном давлении и постоянном объеме равно  для …

Если не учитывать колебательные движения в молекуле водяного пара, то отношение кинетической энергии вращательного движения к полной кинетической энергии молекулы равно …