Для некоторого алгоритма шифрования необходимо подбирать натуральные числа которые можно представить...: ответ на тест 1057915 - Информатика
Для некоторого алгоритма шифрования необходимо подбирать натуральные числа, которые можно представить в виде суммы двух различных простых чисел более чем 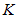 способами, причем все три числа (искомое и оба слагаемых) должны иметь одинаковую разрядность. Например: число 30 подходит для случая
способами, причем все три числа (искомое и оба слагаемых) должны иметь одинаковую разрядность. Например: число 30 подходит для случая 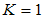 , так как его можно представить в виде
, так как его можно представить в виде 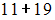 и
и 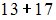 ; число 32 не подходит, потому что представляется всего одной суммой 19+13.
; число 32 не подходит, потому что представляется всего одной суммой 19+13.
Количество подходящих для алгоритма четырехразрядных десятичных чисел при составляет …
составляет …
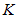 способами, причем все три числа (искомое и оба слагаемых) должны иметь одинаковую разрядность. Например: число 30 подходит для случая
способами, причем все три числа (искомое и оба слагаемых) должны иметь одинаковую разрядность. Например: число 30 подходит для случая 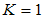 , так как его можно представить в виде
, так как его можно представить в виде 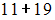 и
и 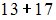 ; число 32 не подходит, потому что представляется всего одной суммой 19+13.
; число 32 не подходит, потому что представляется всего одной суммой 19+13.Количество подходящих для алгоритма четырехразрядных десятичных чисел при
 составляет …
составляет …
Вопрос задал(а): Анонимный пользователь, 13 Ноябрь 2020 в 18:05
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 18:05
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 18:05
