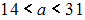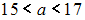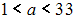Для оценки с некоторой надежностью математического ожидания a нормально распределенного признака X ...: ответ на тест 970272 - Математика и информатика
Для оценки с некоторой надежностью 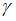 математического ожидания a нормально распределенного признака X по выборочной средней
математического ожидания a нормально распределенного признака X по выборочной средней 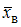 при среднем квадратичном отклонении
при среднем квадратичном отклонении 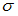 генеральной совокупности использовали доверительный интервал
генеральной совокупности использовали доверительный интервал 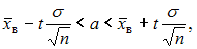 где t – значение аргумента функции Лапласа
где t – значение аргумента функции Лапласа 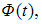 при котором
при котором 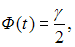 n – объем выборки.
n – объем выборки.
Установите соответствие между значениями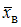 и возможными соответствующими доверительными интервалами:
и возможными соответствующими доверительными интервалами:
1)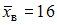
2)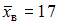
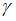 математического ожидания a нормально распределенного признака X по выборочной средней
математического ожидания a нормально распределенного признака X по выборочной средней 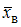 при среднем квадратичном отклонении
при среднем квадратичном отклонении 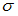 генеральной совокупности использовали доверительный интервал
генеральной совокупности использовали доверительный интервал 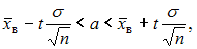 где t – значение аргумента функции Лапласа
где t – значение аргумента функции Лапласа 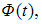 при котором
при котором 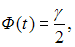 n – объем выборки.
n – объем выборки.Установите соответствие между значениями
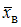 и возможными соответствующими доверительными интервалами:
и возможными соответствующими доверительными интервалами:1)
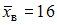
2)
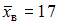
Вопрос задал(а): Анонимный пользователь, 13 Ноябрь 2020 в 16:47
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 16:47
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 16:47