Задание 2 оценивается в 1 балл. На диаграмме процесс проводимый с системой представлен отрезком п...: ответ на тест 882045 - Физика
Задание №2 оценивается в 1 балл.
На диаграмме
 процесс, проводимый с системой, представлен отрезком прямой
процесс, проводимый с системой, представлен отрезком прямой  , где
, где 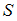 – энтропия системы,
– энтропия системы, 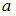 и
и  – константы. Если в ходе обратимого процесса температура
– константы. Если в ходе обратимого процесса температура 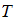 увеличивается от
увеличивается от 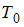 до
до  , то
, то 1) Малое количество теплоты
 , полученное системой при изменении температуры на
, полученное системой при изменении температуры на 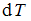 , равно …
, равно …2) Количество теплоты
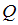 , полученное системой в указанном процессе, определяется выражением …
, полученное системой в указанном процессе, определяется выражением …
Вопрос задал(а): Анонимный пользователь, 13 Ноябрь 2020 в 15:34
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 15:34
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 15:34

 ;
; 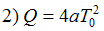
 ;
; 
 ;
; 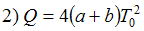
 ;
;