Вопрос № 82156 - Физика
В уравнении Бернулли слагаемое 
где 
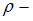плотность жидкости, а 
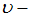скорость ее течения, называется _______ давлением.
где 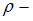плотность жидкости, а 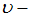скорость ее течения, называется _______ давлением.
Вопрос задал(а): gdaoomewsbjb@dropmail.me, 14 Январь 2016 в 11:37
На вопрос ответил(а): Астафьева Любовь, 14 Январь 2016 в 11:37
На вопрос ответил(а): Астафьева Любовь, 14 Январь 2016 в 11:37
Похожие вопросы
Для однородного стержня закон Гука записывается следующим образом: 
где 
относительное приращение длины стержня, 
модуль Юнга, 
нормальное напряжение. Неверным является утверждение, что …
где относительное приращение длины стержня, модуль Юнга, нормальное напряжение. Неверным является утверждение, что …
модуль Юнга характеризует упругие свойства материала стержня
нормальное напряжение определяется как модуль силы, приходящейся на единицу площади поперечного сечения стержня при условии, что упругая сила распределена равномерно по сечению: 
где значок 
указывает на то, что сила перпендикулярна к площадке, на которую она действует
где значок указывает на то, что сила перпендикулярна к площадке, на которую она действует
модуль Юнга измеряется в 
относительное приращение длины стержня – это отношение длины деформированного стержня к его длине в недеформированном состоянии
В уравнении Бернулли слагаемое 
где 
плотность жидкости, а 
скорость ее течения, называется _______ давлением.
где плотность жидкости, а скорость ее течения, называется _______ давлением.
полным
гидростатическим
статическим
динамическим
Другие вопросы по предмету Физика
На рисунке показаны тела одинаковой массы и размеров, вращающиеся вокруг вертикальных осей. Если частота вращения диска в два раза больше частоты вращения кольца, то отношение кинетических энергий 
равно …
равно …
На рисунке представлен график зависимости от расстояния напряженности поля 
для …
для …
длинного металлического цилиндра (трубы) радиуса R, равномерно заряженного по поверхности
длинного цилиндра радиуса R, равномерно заряженного по объему
металлической сферы радиуса R, равномерно заряженной по поверхности
шара радиуса R, равномерно заряженного по объему
Камень бросили под углом к горизонту со скоростью V0. Его траектория в однородном поле тяжести изображена на рисунке. Сопротивления воздуха нет.
Модуль тангенциального ускорения
на участке С-D-E …
Модуль тангенциального ускорения
на участке С-D-E …
уменьшается
не изменяется
увеличивается
Напряжение на концах медного провода диаметром d и длиной l равно 
. При увеличении напряжения в 4 раза удельная тепловая мощность тока …
. При увеличении напряжения в 4 раза удельная тепловая мощность тока …
не изменится
увеличится в 4 раза
уменьшится в 16 раз
увеличится в 16 раз