Вопрос № 253408 - Физика
На частицу, находящуюся в начале координат, действует сила, вектор которой определяется выражением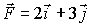 
, где 
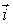и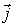 
единичные векторы декартовой системы координат. Работа, совершенная этой силой при перемещении частицы в точку с координатами (0; 5), равна …
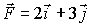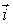, где и 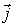единичные векторы декартовой системы координат. Работа, совершенная этой силой при перемещении частицы в точку с координатами (0; 5), равна …
Вопрос задал(а): Анонимный пользователь, 10 Ноябрь 2020 в 00:36
На вопрос ответил(а): Анастасия Степанова, 10 Ноябрь 2020 в 00:36
На вопрос ответил(а): Анастасия Степанова, 10 Ноябрь 2020 в 00:36
Похожие вопросы
На частицу, находящуюся в начале координат, действует сила, вектор которой определяется выражением 
, где 
и 
единичные векторы декартовой системы координат. Работа, совершенная этой силой при перемещении частицы в точку с координатами (4; 3), равна ...
, где и единичные векторы декартовой системы координат. Работа, совершенная этой силой при перемещении частицы в точку с координатами (4; 3), равна ...
9 Дж
16 Дж
12 Дж
25 Дж
На частицу, находящуюся в начале координат, действует сила, вектор которой определяется выражением 
, где 
и 
единичные векторы декартовой системы координат. Работа, совершенная этой силой при перемещении частицы в точку с координатами (4; 3), равна ...
, где и единичные векторы декартовой системы координат. Работа, совершенная этой силой при перемещении частицы в точку с координатами (4; 3), равна ...
16 Дж
12 Дж
9 Дж
25 Дж
Другие вопросы по предмету Физика
На частицу, находящуюся в начале координат, действует сила, вектор которой определяется выражением , где и единичные векторы декартовой системы координат. Работа, совершенная этой силой при перемещении частицы в точку с координатами (4; 3), равна ...
, где и единичные векторы декартовой системы координат. Работа, совершенная этой силой при перемещении частицы в точку с координатами (4; 3), равна ...
16 Дж
12 Дж
9 Дж
25 Дж
На рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где 
– доля молекул, скорости которых заключены в интервале скоростей от v до v+dv в расчете на единицу этого интервала.
Для этой функции верным утверждением является…
– доля молекул, скорости которых заключены в интервале скоростей от v до v+dv в расчете на единицу этого интервала.Для этой функции верным утверждением является…
с ростом температуры площадь под кривой растет
с ростом температуры величина максимума растет
с ростом температуры максимум кривой смещается вправо
На рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где 
– доля молекул, скорости которых заключены в интервале скоростей от v до v+dv в расчете на единицу этого интервала.
Для этой функции верным утверждением является…
– доля молекул, скорости которых заключены в интервале скоростей от v до v+dv в расчете на единицу этого интервала.Для этой функции верным утверждением является…
при изменении температуры площадь под кривой изменяется
с уменьшением температуры величина максимума уменьшается
при изменении температуры площадь под кривой не изменяется
На рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где 
– доля молекул, скорости которых заключены в интервале скоростей от v до v+dv в расчете на единицу этого интервала.
Для этой функции верным утверждением является…
– доля молекул, скорости которых заключены в интервале скоростей от v до v+dv в расчете на единицу этого интервала.Для этой функции верным утверждением является…
при понижении температуры площадь под кривой уменьшается
при понижении температуры величина максимума уменьшается
при понижении температуры максимум кривой смещается влево