Отношение включения двух множеств быть подмножеством обладает различными свойствами в частности сво...: ответ на тест 852575 - Математика
Отношение включения двух множеств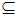 
(быть подмножеством) обладает различными свойствами, в частности, свойством
"если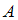
и 
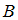– множества, то соотношение 
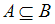и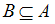 
эквивалентно соотношению 
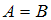" (кратко 
).
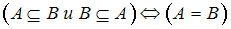Это свойство включения называется …
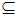(быть подмножеством) обладает различными свойствами, в частности, свойством"есл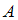и
и 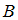– множества, то соотношение 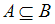и 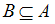эквивалентно соотношению 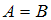" (кратко 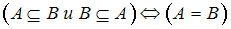).Это свойство включения называется …
Вопрос задал(а): Анонимный пользователь, 13 Ноябрь 2020 в 15:19
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 15:19
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 15:19