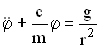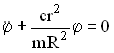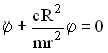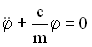Механическая система с одной степенью свободы совершает малые колебания. За обобщенную координату пр...: ответ на тест 596035 - Теоретическая механика
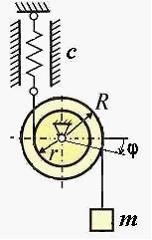
Механическая система с одной степенью свободы совершает малые колебания. За обобщенную координату принят угол поворота шкива j. Система состоит из ступенчатого шкива с отношением радиусов 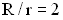 , груза массы m и пружины жесткости С. На рисунке механизм находится в равновесии при
, груза массы m и пружины жесткости С. На рисунке механизм находится в равновесии при 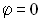 .
.
 Принять:
Принять: 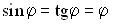 ,
, 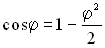 , считать
, считать 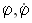 - малыми, массой шкива пренебрегаем.
- малыми, массой шкива пренебрегаем.
Записать дифференциальное уравнение малых колебаний (Уравнение Лагранжа – II рода).
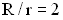 , груза массы m и пружины жесткости С. На рисунке механизм находится в равновесии при
, груза массы m и пружины жесткости С. На рисунке механизм находится в равновесии при 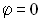 .
. Принять:
Принять: 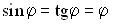 ,
, 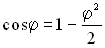 , считать
, считать 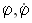 - малыми, массой шкива пренебрегаем.
- малыми, массой шкива пренебрегаем.Записать дифференциальное уравнение малых колебаний (Уравнение Лагранжа – II рода).
Вопрос задал(а): Анонимный пользователь, 10 Ноябрь 2020 в 20:31
На вопрос ответил(а): Анастасия Степанова, 10 Ноябрь 2020 в 20:31
На вопрос ответил(а): Анастасия Степанова, 10 Ноябрь 2020 в 20:31