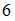О функции известна информация представленная в таблице . Функция интерполируется кубическим сплайн...: ответ на тест 853069 - Математика
О функции 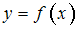 известна информация, представленная в таблице
известна информация, представленная в таблице
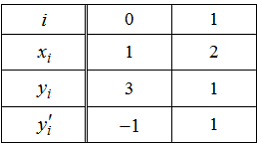 .
.
Функция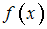 интерполируется кубическим сплайном
интерполируется кубическим сплайном 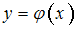 , где
, где 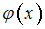 – полином 3-й степени, причём в узлах интерполяции
– полином 3-й степени, причём в узлах интерполяции 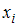 ,
, 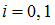 , должны выполняться условия
, должны выполняться условия 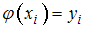 ,
, 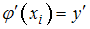 .
.
Тогда значения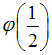 и
и 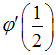 соответственно равны …
соответственно равны …
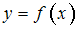 известна информация, представленная в таблице
известна информация, представленная в таблице .
.Функция
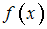 интерполируется кубическим сплайном
интерполируется кубическим сплайном 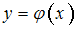 , где
, где 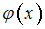 – полином 3-й степени, причём в узлах интерполяции
– полином 3-й степени, причём в узлах интерполяции 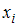 ,
, 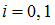 , должны выполняться условия
, должны выполняться условия 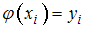 ,
, 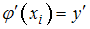 .
.Тогда значения
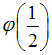 и
и 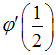 соответственно равны …
соответственно равны …
Вопрос задал(а): Анонимный пользователь, 13 Ноябрь 2020 в 15:19
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 15:19
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 15:19

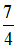 и
и 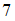
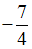 и
и 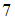
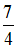 и
и 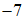
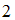 и
и