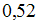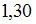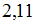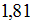Для приближенного решения дифференциального уравнения с начальным условием можно воспользоваться м...: ответ на тест 910469 - Математика
Для приближенного решения дифференциального уравнения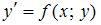 
с начальным условием 
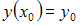можно воспользоваться методом Эйлера: 
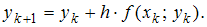Тогда для уравнения 
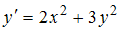при начальном условии 
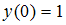с шагом 
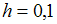значение 
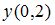с точностью до сотых равно …
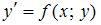с начальным условием 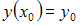можно воспользоваться методом Эйлера: 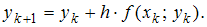Тогда для уравнения 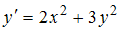при начальном условии 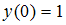с шагом 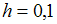значение 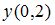с точностью до сотых равно … 
Вопрос задал(а): Анонимный пользователь, 13 Ноябрь 2020 в 16:10
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 16:10
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 16:10