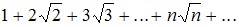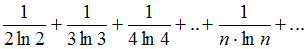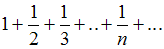Вопрос № 880582 - Математика
Исследуйте на сходимость числовые ряды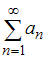 
.
Можно воспользоваться интегральным признаком сходимости рядов.
(Пусть f(x) такая функция, что f(n)=an. Если
сходится, то сходится и соответствующий числовой ряд).
Сходящимся является ряд …
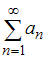.Можно воспользоваться интегральным признаком сходимости рядов.
(Пусть f(x) такая функция, что f(n)=an. Если
сходится, то сходится и соответствующий числовой ряд).Сходящимся является ряд …
Вопрос задал(а): Анонимный пользователь, 13 Ноябрь 2020 в 15:33
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 15:33
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 15:33
Похожие вопросы
Исследуйте на сходимость числовые ряды 
.
Можно воспользоваться признаком сравнения рядов:
пусть для рядов
и 
выполняется условие:
для всех n >N , где N – некоторое натуральное число.
Тогда:
1. Если ряд
расходится, то расходится и ряд 
2. Если ряд
сходится, то сходится и ряд 
В данных задачах за ряд
можно взять расходящийся ряд 
и сходящийся ряд
.
В этом случае сходящимся является ряд …
.Можно воспользоваться признаком сравнения рядов:
пусть для рядов
и выполняется условие: для всех n >N , где N – некоторое натуральное число.Тогда:
1. Если ряд
расходится, то расходится и ряд 2. Если ряд
сходится, то сходится и ряд В данных задачах за ряд
можно взять расходящийся ряд и сходящийся ряд
.В этом случае сходящимся является ряд …
Исследуйте на сходимость числовые ряды 
.
Можно воспользоваться признаком Коши:
Сходящимся является ряд …
.Можно воспользоваться признаком Коши:
Сходящимся является ряд …
Другие вопросы по предмету Математика
Исследуйте на сходимость числовые ряды .
Можно воспользоваться признаком сравнения рядов:
пусть для рядов и выполняется условие:
для всех n >N , где N – некоторое натуральное число.
Тогда:
1. Если рядрасходится, то расходится и ряд
2. Если рядсходится, то сходится и ряд
В данных задачах за ряд можно взять расходящийся ряд
и сходящийся ряд.
В этом случае сходящимся является ряд …
.Можно воспользоваться признаком сравнения рядов:
пусть для рядов
и выполняется условие: для всех n >N , где N – некоторое натуральное число.Тогда:
1. Если ряд
расходится, то расходится и ряд 2. Если ряд
сходится, то сходится и ряд В данных задачах за ряд
можно взять расходящийся ряд и сходящийся ряд
.В этом случае сходящимся является ряд …
Исследуйте на сходимость числовые ряды 
.
Расходящимся является ряд…
.Расходящимся является ряд…
У степенного ряда 
радиус сходимости R равен …
радиус сходимости R равен …
0
2
У степенного ряда 
радиус сходимости R равен …
радиус сходимости R равен …
0
n
1