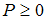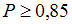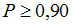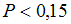Вероятность появления события в каждом из 250 проведенных испытаний равна 04. Тогда вероятность тог...: ответ на тест 1027119 - Теория вероятностей и математическая статистика
Вероятность появления события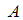 
в каждом из 250 проведенных испытаний равна 0,4. Тогда вероятность того, что число 
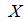появлений события 
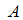будет заключено в пределах от 80 до 120, можно оценить с использованием неравенства Чебышева как …
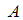в каждом из 250 проведенных испытаний равна 0,4. Тогда вероятность того, что число 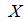появлений события 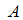будет заключено в пределах от 80 до 120, можно оценить с использованием неравенства Чебышева как … 
Вопрос задал(а): Анонимный пользователь, 13 Ноябрь 2020 в 17:28
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 17:28
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 17:28