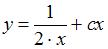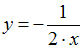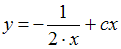Дифференциальное уравнение вида: называется дифференциальным уравнением первого порядка. Для решени...: ответ на тест 880571 - Математика
Дифференциальное уравнение вида:  называется дифференциальным уравнением первого порядка. Для решения уравнения
называется дифференциальным уравнением первого порядка. Для решения уравнения
такого типа используют подстановку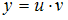 , тогда
, тогда 
Сделав подстановку в исходное уравнение, нужно вынести за скобки
и выражение, стоящее в скобках, приравнять к нулю.
Решив полученное дифференциальное уравнение, найдем
Затем решаем оставшееся дифференциальное уравнение с разделяющимися переменными.
Тогда решением (общим интегралом) дифференциального уравнения
 является …
является …
 называется дифференциальным уравнением первого порядка. Для решения уравнения
называется дифференциальным уравнением первого порядка. Для решения уравнениятакого типа используют подстановку
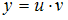 , тогда
, тогда 
Сделав подстановку в исходное уравнение, нужно вынести за скобки

и выражение, стоящее в скобках, приравнять к нулю.
Решив полученное дифференциальное уравнение, найдем

Затем решаем оставшееся дифференциальное уравнение с разделяющимися переменными.
Тогда решением (общим интегралом) дифференциального уравнения
 является …
является …
Вопрос задал(а): Анонимный пользователь, 13 Ноябрь 2020 в 15:33
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 15:33
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 15:33