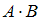Два студента сдают экзамен. Если ввести события экзамен успешно сдал первый студент и экзамен успешн...: ответ на тест 1027067 - Теория вероятностей и математическая статистика
Два студента сдают экзамен. Если ввести события  (экзамен успешно сдал первый студент) и
(экзамен успешно сдал первый студент) и  (экзамен успешно сдал второй студент), то событие, заключающееся в том, что экзамен успешно сдаст только один студент, будет представлять собой выражение …
(экзамен успешно сдал второй студент), то событие, заключающееся в том, что экзамен успешно сдаст только один студент, будет представлять собой выражение …
 (экзамен успешно сдал первый студент) и
(экзамен успешно сдал первый студент) и  (экзамен успешно сдал второй студент), то событие, заключающееся в том, что экзамен успешно сдаст только один студент, будет представлять собой выражение …
(экзамен успешно сдал второй студент), то событие, заключающееся в том, что экзамен успешно сдаст только один студент, будет представлять собой выражение …
Вопрос задал(а): Анонимный пользователь, 13 Ноябрь 2020 в 17:28
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 17:28
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 17:28