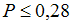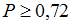Вопрос № 1029723 - Теория вероятностей и математическая статистика
Математическое ожидание случайной величины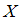 
равно 
, а дисперсия –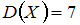 
. Тогда вероятность того, что 
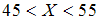, можно оценить с использованием неравенства Чебышева как …
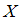равно , а дисперсия – 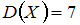. Тогда вероятность того, что 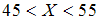, можно оценить с использованием неравенства Чебышева как … 
Вопрос задал(а): Анонимный пользователь, 13 Ноябрь 2020 в 17:31
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 17:31
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 17:31
Похожие вопросы
Математическое ожидание случайной величины X равно 
а дисперсия – 
Тогда вероятность того, что 
можно оценить с использованием неравенства Чебышева как …
а дисперсия – Тогда вероятность того, что можно оценить с использованием неравенства Чебышева как … 
Математическое ожидание случайной величины X равно 
а дисперсия – 
Тогда вероятность того, что 
можно оценить с использованием неравенства Чебышева как …
а дисперсия – Тогда вероятность того, что можно оценить с использованием неравенства Чебышева как … 
Другие вопросы по предмету Теория вероятностей и математическая статистика
В результате проведения 100 независимых испытаний получены случайные величины 
с равными математическими ожиданиями 
и равными дисперсиями 
. Тогда вероятность того, что среднее арифметическое этих случайных величин отклонится по абсолютной величине от математического ожидания 
на величину, меньшую 
, можно оценить как …
с равными математическими ожиданиями и равными дисперсиями . Тогда вероятность того, что среднее арифметическое этих случайных величин отклонится по абсолютной величине от математического ожидания на величину, меньшую , можно оценить как … 
В результате проведения 200 независимых испытаний получены случайные величины 
с равными математическими ожиданиями 
и равными дисперсиями 
. Тогда вероятность того, что среднее арифметическое этих случайных величин отклонится по абсолютной величине от математического ожидания 
на величину, меньшую 
, можно оценить как …
с равными математическими ожиданиями и равными дисперсиями . Тогда вероятность того, что среднее арифметическое этих случайных величин отклонится по абсолютной величине от математического ожидания на величину, меньшую , можно оценить как … 
В результате проведения 100 независимых испытаний получены случайные величины 
с равными математическими ожиданиями 
и равными дисперсиями 
. Тогда вероятность того, что среднее арифметическое этих случайных величин отклонится по абсолютной величине от математического ожидания 
на величину, меньшую 
, можно оценить как …
с равными математическими ожиданиями и равными дисперсиями . Тогда вероятность того, что среднее арифметическое этих случайных величин отклонится по абсолютной величине от математического ожидания на величину, меньшую , можно оценить как … 
В результате проведения 200 независимых испытаний получены случайные величины 
с равными математическими ожиданиями 
и равными дисперсиями 
. Тогда вероятность того, что среднее арифметическое этих случайных величин отклонится по абсолютной величине от математического ожидания 
на величину, меньшую 
, можно оценить как …
с равными математическими ожиданиями и равными дисперсиями . Тогда вероятность того, что среднее арифметическое этих случайных величин отклонится по абсолютной величине от математического ожидания на величину, меньшую , можно оценить как … 
