Вопрос № 882012 - Математика
Пусть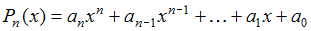 
многочлен наименьшей степени, имеющий минимум равный –60 при x= –4 и максимум равный 48 при x = 2. Тогда сумма коэффициентов многочлена 
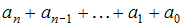равна …
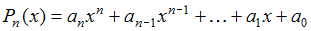многочлен наименьшей степени, имеющий минимум равный –60 при x= –4 и максимум равный 48 при x = 2. Тогда сумма коэффициентов многочлена 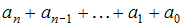равна …
Вопрос задал(а): Анонимный пользователь, 13 Ноябрь 2020 в 15:34
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 15:34
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 15:34
Похожие вопросы
Пусть 
– многочлен наименьшей степени, имеющий минимум, равный (–60) при x = –4, и максимум, равный 48 при x = 2. Тогда сумма коэффициентов многочлена 
равна …
– многочлен наименьшей степени, имеющий минимум, равный (–60) при x = –4, и максимум, равный 48 при x = 2. Тогда сумма коэффициентов многочлена равна …
Пусть 
многочлен наименьшей степени, имеющий минимум равный 
при 
и максимум равный 17 при 
. Тогда сумма коэффициентов многочлена 
равна …
многочлен наименьшей степени, имеющий минимум равный при и максимум равный 17 при . Тогда сумма коэффициентов многочлена равна … Другие вопросы по предмету Математика
Пусть многочлен наименьшей степени, имеющий минимум равный при и максимум равный 17 при . Тогда сумма коэффициентов многочлена равна …
многочлен наименьшей степени, имеющий минимум равный при и максимум равный 17 при . Тогда сумма коэффициентов многочлена равна …
Пусть 
многочлен наименьшей степени, имеющий минимум равный 
при 
и максимум равный 
при 
. Тогда сумма коэффициентов многочлена 
равна …
многочлен наименьшей степени, имеющий минимум равный при и максимум равный при . Тогда сумма коэффициентов многочлена равна …
Пусть 
многочлен наименьшей степени, имеющий минимум равный 
при 
и максимум равный 
при 
. Тогда сумма коэффициентов многочлена 
равна …
многочлен наименьшей степени, имеющий минимум равный при и максимум равный при . Тогда сумма коэффициентов многочлена равна …
Пусть 
многочлен наименьшей степени, имеющий минимум равный 
при 
и максимум равный 
при 
Тогда сумма коэффициентов многочлена 
равна …
многочлен наименьшей степени, имеющий минимум равный при и максимум равный при Тогда сумма коэффициентов многочлена равна …