Уравнение является: ответ на тест 1026994 - Математический анализ
Уравнение 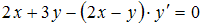 является …
является …
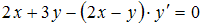 является …
является …
Вопрос задал(а): Анонимный пользователь, 13 Ноябрь 2020 в 17:28
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 17:28
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 17:28

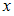 и
и 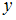 дифференциальным уравнением первого порядка
дифференциальным уравнением первого порядка