Пусть рассматриваются две случайных величины и . Для них вычислены коэффициент парной линейной регр...: ответ на тест 718974 - Эконометрика
Пусть рассматриваются две случайных величины  и
и 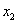 . Для них вычислены коэффициент парной линейной регрессии
. Для них вычислены коэффициент парной линейной регрессии 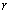 и корреляционное отношение по уравнению связи
и корреляционное отношение по уравнению связи  . Известно, что
. Известно, что  . Это означает, что между величинами …
. Это означает, что между величинами …
 и
и 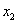 . Для них вычислены коэффициент парной линейной регрессии
. Для них вычислены коэффициент парной линейной регрессии 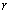 и корреляционное отношение по уравнению связи
и корреляционное отношение по уравнению связи  . Известно, что
. Известно, что  . Это означает, что между величинами …
. Это означает, что между величинами …
Вопрос задал(а): Анонимный пользователь, 13 Ноябрь 2020 в 00:25
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 00:25
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 00:25
