Вопрос № 861024 - Математика
Пусть бесконечно дифференцируемая функция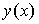 
такая, что 
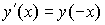и 
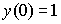. Тогда значение выражения 
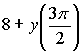равно …
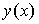такая, что 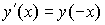и 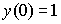. Тогда значение выражения 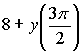равно …
Вопрос задал(а): Анонимный пользователь, 13 Ноябрь 2020 в 15:22
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 15:22
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 15:22
Похожие вопросы
Пусть бесконечно дифференцируемая функция 
такая, что 
и 
. Тогда значение выражения 
равно …
такая, что и . Тогда значение выражения равно …
Бесконечно дифференцируемая функция 
такая, что 
для всех 
и 
. Тогда 
равно …
такая, что для всех и . Тогда равно … Другие вопросы по предмету Математика
Пусть матрица А является матрицей размера 
такой, что 
и 
. Тогда сумма всех элементов матрицы 
равна…
такой, что и . Тогда сумма всех элементов матрицы равна…
Последовательность 
задана рекуррентным соотношением: 
, 
, 
при 
. Пусть N – номер равного нулю члена этой последовательности (
). Тогда N равно…
задана рекуррентным соотношением: , , при . Пусть N – номер равного нулю члена этой последовательности (). Тогда N равно…
Пусть 
. Тогда значение предела 
равно…
. Тогда значение предела равно…
Пусть матрица А равна: 
, где m – натуральное число. При каком значении m сумма всех элементов первой строки этой матрицы будет максимальной?
, где m – натуральное число. При каком значении m сумма всех элементов первой строки этой матрицы будет максимальной?