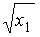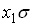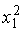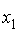Вопрос № 579255 - Эконометрика
Пусть в модели линейной регрессии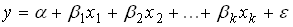 
нарушено одно из условий Гаусса-Маркова: математическое ожидание ошибок равно 0 
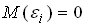, а дисперсия остатков 
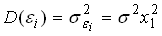пропорциональна величине 
, 
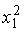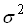– неизвестная постоянная, характеризующая дисперсию ошибки при соблюдении предпосылки о гетероскедастичности. Для перехода к уравнению с гомоскедастичными остатками все переменные уравнения необходимо поделить на величину…
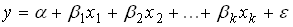нарушено одно из условий Гаусса-Маркова: математическое ожидание ошибок равно 0 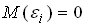, а дисперсия остатков 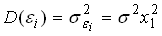пропорциональна величине 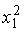, 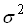– неизвестная постоянная, характеризующая дисперсию ошибки при соблюдении предпосылки о гетероскедастичности. Для перехода к уравнению с гомоскедастичными остатками все переменные уравнения необходимо поделить на величину… 
Вопрос задал(а): Анонимный пользователь, 10 Ноябрь 2020 в 19:44
На вопрос ответил(а): Анастасия Степанова, 10 Ноябрь 2020 в 19:44
На вопрос ответил(а): Анастасия Степанова, 10 Ноябрь 2020 в 19:44
Похожие вопросы
Пусть в модели линейной регрессии 
нарушено одно из условий Гаусса-Маркова: математическое ожидание ошибок равно 0 
, а дисперсия остатков 
пропорциональна величине 
, 
– неизвестная постоянная, характеризующая дисперсию ошибки при соблюдении предпосылки о гетероскедастичности. Для перехода к уравнению с гомоскедастичными остатками все переменные уравнения необходимо поделить на величину…
нарушено одно из условий Гаусса-Маркова: математическое ожидание ошибок равно 0 , а дисперсия остатков пропорциональна величине , – неизвестная постоянная, характеризующая дисперсию ошибки при соблюдении предпосылки о гетероскедастичности. Для перехода к уравнению с гомоскедастичными остатками все переменные уравнения необходимо поделить на величину… 
Пусть в модели линейной регрессии 
нарушено одно из условий Гаусса-Маркова: математическое ожидание ошибок равно 0 
, а дисперсия остатков 
пропорциональна величине 
, меняющейся с изменением какого-то фактора, 
– неизвестная постоянная, характеризующая дисперсию ошибки при соблюдении предпосылки о гетероскедастичности. Для перехода к уравнению с гомоскедастичными остатками все переменные уравнения необходимо поделить на величину…
нарушено одно из условий Гаусса-Маркова: математическое ожидание ошибок равно 0 , а дисперсия остатков пропорциональна величине , меняющейся с изменением какого-то фактора, – неизвестная постоянная, характеризующая дисперсию ошибки при соблюдении предпосылки о гетероскедастичности. Для перехода к уравнению с гомоскедастичными остатками все переменные уравнения необходимо поделить на величину… 
Другие вопросы по предмету Эконометрика
Укажите последовательность этапов проведения теста Голдфелда-Квандта для парной линейной регрессии
упорядочение наблюдений по возрастанию значений объясняющей переменной
оценка регрессий для k-первых и k-последних наблюдений
оценка сумм квадратов отклонений для регрессий по k-первым и k-последним наблюдений
вычисление статистики Фишера
Пусть в модели yi=b0+b1xi+ei случайные отклонения ei гетероскедастичны. При этом обнаружено, что дисперсия отклонений ei пропорциональна значениям 
. Укажите последовательность этапов одного из методов устранения гетероскедастичности
. Укажите последовательность этапов одного из методов устранения гетероскедастичности
выдвигается гипотеза, что дисперсии отклонений пропорциональны значениям 
. Вводится коэффициент пропорциональности 
. Вводится коэффициент пропорциональности
строится регрессия новой зависимой переменной 
на новую независимую переменную 
на новую независимую переменную
оцениваются коэффициенты новой регрессии и их статистическая значимость
оценивается общее качество преобразованной модели
Укажите последовательность этапов обобщенного метода наименьших квадратов
устанавливается наличие гетероскедастичности или автокорреляции остатков
изменяется спецификация модели (путем преобразования уравнения с учетом коэффициента пропорциональности дисперсий остатков)
оцениваются параметры новой модели и их статистическая значимость
оценивается общее качество преобразованной модели
Коэффициент корреляции признаков y и x, рассчитанный по уравнению связи 
имеет ту же размерность, что и 
имеет ту же размерность, что и 
имеет ту же размерность, что и 
является безразмерным