Вопрос № 860307 - Математика
Для функции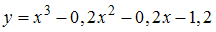 
требуется методом хорд (секущих) найти корень на отрезке 
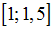. Начальное приближение 
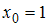. Следует найти только приближения 
, 
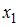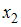и оценить погрешность 
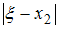, где 
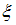– точное значение корня.
Тогда приближение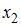
и погрешность равны соответственно …
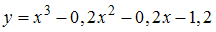требуется методом хорд (секущих) найти корень на отрезке 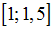. Начальное приближение 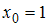. Следует найти только приближения 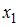, 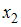и оценить погрешность 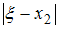, где 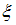– точное значение корня.Тогда приближение
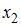и погрешность равны соответственно …
Вопрос задал(а): Анонимный пользователь, 13 Ноябрь 2020 в 15:22
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 15:22
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 15:22
Похожие вопросы
Для функции 
требуется методом хорд (секущих) найти корень на отрезке 
. Начальное приближение 
. Следует найти только приближения 
, 
и оценить погрешность 
, где 
– точное значение корня.
Тогда приближение
и погрешность равны соответственно …
требуется методом хорд (секущих) найти корень на отрезке . Начальное приближение . Следует найти только приближения , и оценить погрешность , где – точное значение корня.Тогда приближение
и погрешность равны соответственно …
1,195 и 0,076
1,144 и 0,021
1,187 и 0,097
1,187 и 0,058
Дана система уравнений
Требуется систему уравнений преобразовать в приведённую систему, взять начальное приближение
, 
, 
и выполнить два шага (т.е. найти второе приближение к решению) метода Зейделя.
Тогда компоненты
и 
второго приближения к решению соответственно равны …
Требуется систему уравнений преобразовать в приведённую систему, взять начальное приближение
, , и выполнить два шага (т.е. найти второе приближение к решению) метода Зейделя.Тогда компоненты
и второго приближения к решению соответственно равны … 
и 
и 
и 
и 
Другие вопросы по предмету Математика
Наименьший корень уравнения 
принадлежит интервалу …
принадлежит интервалу … 
Число действительных корней уравнения 
равно …
равно …
0
1
3
2
Пусть 
– алгебраическая или трансцендентная функция:
1) определённая на отрезке
,
2) имеющая на отрезке
непрерывные производные 
и 
, сохраняющие знак на этом отрезке,
3) имеющая единственный корень
на отрезке 
.
Этот корень необходимо найти приближённо, используя метод Ньютона (касательных).
Тогда выбор начального приближения
, вычисление приближений 
и оценка погрешности осуществляются соответственно по следующим формулам:
– алгебраическая или трансцендентная функция:1) определённая на отрезке
, 2) имеющая на отрезке
непрерывные производные и , сохраняющие знак на этом отрезке,3) имеющая единственный корень
на отрезке .Этот корень необходимо найти приближённо, используя метод Ньютона (касательных).
Тогда выбор начального приближения
, вычисление приближений и оценка погрешности осуществляются соответственно по следующим формулам: 
; 
, 
; 
; 
, 
; 
; 
, 
; 
; 
, 
; 
Методом Эйлера решается задача Коши
на отрезке
.
Выбрав начальный шаг
, найдите 
с точностью 
(ошибки округления не учитывать).
Тогда значение
равно …
на отрезке
.Выбрав начальный шаг
, найдите с точностью (ошибки округления не учитывать).Тогда значение
равно …
– 0,09
– 0,10
– 0,12
– 0,11