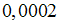Вопрос № 860299 - Математика
Функция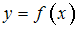 
представлена таблицей
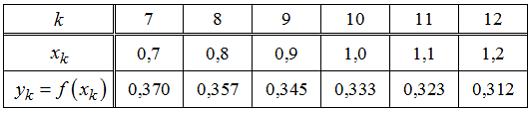
Значение интеграла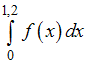
вычисляется методом Симпсона, а точность (погрешность) оценивается по методу Рунге – Ромберга. Погрешностями округлений пренебрегают.
Тогда значения интеграла и погрешности соответственно равны …
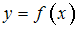представлена таблицейЗначение интеграла
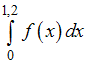вычисляется методом Симпсона, а точность (погрешность) оценивается по методу Рунге – Ромберга. Погрешностями округлений пренебрегают.Тогда значения интеграла и погрешности соответственно равны …
и 
и 
и 
и 
Вопрос задал(а): Анонимный пользователь, 13 Ноябрь 2020 в 15:22
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 15:22
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 15:22
Похожие вопросы
Функция 
представлена таблицей
Значение интеграла
вычисляется методом Симпсона, а точность (погрешность) оценивается по методу Рунге – Ромберга. Погрешностями округлений пренебрегают.
Тогда значения интеграла и погрешности соответственно равны …
представлена таблицейЗначение интеграла
вычисляется методом Симпсона, а точность (погрешность) оценивается по методу Рунге – Ромберга. Погрешностями округлений пренебрегают.Тогда значения интеграла и погрешности соответственно равны …
и 
и 
и 
и 
Для функции 
известны её значения в узлах 
, 
, 
, 
. Требуется вычислить значение этой функции в точке 
.
Для вычисления
используется интерполяционный полином Лагранжа 
3-й степени. Погрешностями округлений пренебрегают.
Тогда величина
не превышает …
известны её значения в узлах , , , . Требуется вычислить значение этой функции в точке .Для вычисления
используется интерполяционный полином Лагранжа 3-й степени. Погрешностями округлений пренебрегают.Тогда величина
не превышает … 
Другие вопросы по предмету Математика
Интеграл 
вычисляется с использованием составной формулы Симпсона, а погрешность вычисления оценивается с использованием производных. Погрешностью округления пренебрегают.
Заданная точность вычислений равна
.
Тогда для выполнения требований задачи величина шага (с тремя знаками после запятой) не должна превышать числа …
вычисляется с использованием составной формулы Симпсона, а погрешность вычисления оценивается с использованием производных. Погрешностью округления пренебрегают.Заданная точность вычислений равна
.Тогда для выполнения требований задачи величина шага (с тремя знаками после запятой) не должна превышать числа …
Для оценки погрешности интерполяции сплайнами в некоторых случаях используется модуль непрерывности функции.
Тогда при
значение модуля непрерывности функции 
, рассматриваемой на отрезке 
, равно …
Тогда при
значение модуля непрерывности функции , рассматриваемой на отрезке , равно … 
Пусть для функции 
заданы значения: 
, 
, 
. Функция интерполируется квадратичным сплайном 
, причём должны выполняться условия:
1) в узлах интерполяции
;
2) производная
непрерывна на отрезке 
;
3)
.
Тогда значения сплайна
и его производной 
равны соответственно …
заданы значения: , , . Функция интерполируется квадратичным сплайном , причём должны выполняться условия: 1) в узлах интерполяции
; 2) производная
непрерывна на отрезке ;3)
.Тогда значения сплайна
и его производной равны соответственно … 
и 
и 
и 
и 
О функции 
известна информация, представленная в таблице
.
Функция
интерполируется кубическим сплайном 
, где 
– полином 3-й степени, причём в узлах интерполяции 
, 
, должны выполняться условия 
, 
.
Тогда значения
и 
соответственно равны …
известна информация, представленная в таблице.Функция
интерполируется кубическим сплайном , где – полином 3-й степени, причём в узлах интерполяции , , должны выполняться условия , .Тогда значения
и соответственно равны … 
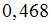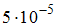
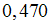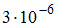
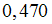и 
и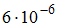 
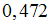и 
и 