Для регрессионной модели где – нелинейная функция – рассчитанное по модели значение переменной п...: ответ на тест 1026071 - Эконометрика
Для регрессионной модели 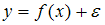 , где
, где 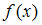 – нелинейная функция,
– нелинейная функция,  – рассчитанное по модели значение переменной
– рассчитанное по модели значение переменной 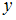 , получены значения дисперсий:
, получены значения дисперсий: 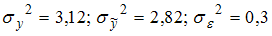 . Не объяснена моделью часть дисперсии переменной
. Не объяснена моделью часть дисперсии переменной 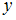 , равная …
, равная …
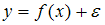 , где
, где 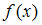 – нелинейная функция,
– нелинейная функция,  – рассчитанное по модели значение переменной
– рассчитанное по модели значение переменной 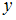 , получены значения дисперсий:
, получены значения дисперсий: 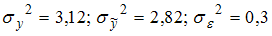 . Не объяснена моделью часть дисперсии переменной
. Не объяснена моделью часть дисперсии переменной 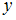 , равная …
, равная …
Вопрос задал(а): Анонимный пользователь, 13 Ноябрь 2020 в 17:27
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 17:27
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 17:27
