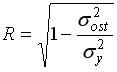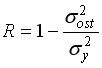Уравнение нелинейной регрессии где — общая дисперсия результативного признака ; — остаточная дисп...: ответ на тест 719588 - Эконометрика
Уравнение нелинейной регрессии 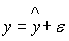 , где
, где 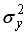 — общая дисперсия результативного признака
— общая дисперсия результативного признака 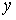 ;
; 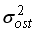 — остаточная дисперсия ошибки
— остаточная дисперсия ошибки  , может оцениваться показателем тесноты связи – индексом корреляции
, может оцениваться показателем тесноты связи – индексом корреляции 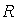 , который вычисляется по формуле …
, который вычисляется по формуле …
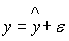 , где
, где 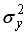 — общая дисперсия результативного признака
— общая дисперсия результативного признака 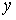 ;
; 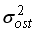 — остаточная дисперсия ошибки
— остаточная дисперсия ошибки  , может оцениваться показателем тесноты связи – индексом корреляции
, может оцениваться показателем тесноты связи – индексом корреляции 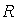 , который вычисляется по формуле …
, который вычисляется по формуле …
Вопрос задал(а): Анонимный пользователь, 13 Ноябрь 2020 в 00:25
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 00:25
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 00:25