Для приближенного вычисления интеграла можно воспользоваться формулой трапеций: Отрезок a;b разбит ...: ответ на тест 880267 - Математика
Для приближенного вычисления интеграла можно воспользоваться формулой трапеций: 
Отрезок [a;b] разбит на n равных частей.
Пусть n=4. Вычисления производите с точностью до 0,01.
Тогда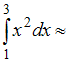
…
Отрезок [a;b] разбит на n равных частей.
Пусть n=4. Вычисления производите с точностью до 0,01.
Тогда
…
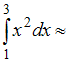Вопрос задал(а): Анонимный пользователь, 13 Ноябрь 2020 в 15:33
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 15:33
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 15:33
Похожие вопросы
Для приближенного вычисления интеграла можно воспользоваться формулой трапеций: 
Отрезок [a;b] разбит на n равных частей.
Пусть n=4. Вычисления производите с точностью до 0,01.
Известны значения функции sinx в точках:
Тогда
…
Отрезок [a;b] разбит на n равных частей.
Пусть n=4. Вычисления производите с точностью до 0,01.
Известны значения функции sinx в точках:
Тогда
…
0,4
0,3103
0,35
0,32
Для приближенного вычисления интеграла можно воспользоваться формулой трапеций: 
Отрезок [a;b] разбит на n равных частей.
Пусть n=4. Вычисления производите с точностью до 0,01.
Известны значения функции
в точках:
Тогда
…
Отрезок [a;b] разбит на n равных частей.
Пусть n=4. Вычисления производите с точностью до 0,01.
Известны значения функции
в точках:Тогда
…
0,7
0,75
0,7468
0,74
Другие вопросы по предмету Математика
Для приближенного вычисления интеграла можно воспользоваться
формулой трапеций:
Отрезок [a;b] разбит на n равных частей.
Пусть n=4. Вычисления производите с точностью до 0,01.
Известны значения функции
в точках:
Тогда
…
формулой трапеций:
Отрезок [a;b] разбит на n равных частей.
Пусть n=4. Вычисления производите с точностью до 0,01.
Известны значения функции
в точках:Тогда
…
Для приближенного вычисления интеграла можно воспользоваться формулой трапеций: 
Отрезок [a;b] разбит на n равных частей.
Пусть n=4. Вычисления производите с точностью до 0,01.
Известны значения функции
в точках:
Тогда
…
Отрезок [a;b] разбит на n равных частей.
Пусть n=4. Вычисления производите с точностью до 0,01.
Известны значения функции
в точках:Тогда
…
Для приближенного вычисления интеграла можно воспользоваться формулой трапеций:
Отрезок [a;b] разбит на n равных частей.
Пусть n=4. Вычисления производите с точностью до 0,01.
Известны значения функции в точках:
Тогда …
Отрезок [a;b] разбит на n равных частей.
Пусть n=4. Вычисления производите с точностью до 0,01.
Известны значения функции
в точках:Тогда
…
Для приближенного вычисления интеграла можно воспользоваться формулой трапеций:
Отрезок [a;b] разбит на n равных частей.
Пусть n=4. Вычисления производите с точностью до 0,01.
Известны значения функции sinx в точках:
Тогда …
Отрезок [a;b] разбит на n равных частей.
Пусть n=4. Вычисления производите с точностью до 0,01.
Известны значения функции sinx в точках:
Тогда
… Все Предметы (168)
- Административное право
- Анализ финансово-хозяйственной деятельности
- Анатомия
- Английский язык
- Арбитражный процесс
- Архитектура
- Базы данных
- Безопасность жизнедеятельности
- Биология
- Ботаника
- Бухгалтерский учет
- Бухгалтерский финансовый учет
- Бюджетное право
- Возрастная анатомия
- Возрастная физиология
- Вычислительная математика
- Вычислительная техника
- Генетика
- География
- Геодезия
- Гидравлика
- Гистология, эмбриология и цитология
- Гражданское право
- Гражданское процессуальное право
- Демография
- Деньги, кредит, банки
- Детали машин и основы конструирования
- Диагностика готовности первокурсников к продолжению обучения
- Дискретная математика
- Естественнонаучная картина мира
- Защита растений
- Земельное право
- Земледелие
- Инженерная геодезия
- Инженерная геология
- Инженерная графика
- Инженерная и компьютерная графика
- Иностранный язык
- Информатика
- Информационные технологии в профессиональной деятельности
- Информационные технологии в юридической деятельности
- Информационные технологии управления
- История
- История государства и права
- История государства и права зарубежных стран
- История и философия науки
- История изучаемого региона
- История образования и педагогической мысли
- История политических и правовых учений
- История России
- История философии
- Коммерческое право
- Конституционное право зарубежных стран
- Конституционное право России
- Конструкция и проектирование летательных аппаратов
- Конфликтология
- Концепции современного естествознания
- Криминалистика
- Культурология
- Линейная алгебра
- Логика
- Макроэкономика
- Маркетинг
- Математика
- Математика и информатика
- Математический анализ
- Материаловедение
- Международное право
- Международное частное право
- Менеджмент
- Метрология, стандартизация и сертификация
- Механика грунтов
- Микробиология
- Микробиология и иммунология
- Микробиология, вирусология и иммунология
- Микроэкономика
- Мировая экономика
- Мировые информационные ресурсы
- Морфология животных
- Морфология сельскохозяйственных животных
- Налоговое право
- Наследственное право
- Национальная экономика
- Начертательная геометрия
- Начертательная геометрия, инженерная графика
- Немецкий язык
- Неорганическая химия
- Общая электротехника и электроника
- Обществознание
- Олимпиада математика, физика и информатика
- Основы безопасности жизнедеятельности
- Основы бухгалтерского учета
- Основы медицинских знаний и здорового образа жизни
- Основы почвоведения и сельскохозяйственного производства
- Основы права
- Основы социологии и политологии
- Основы специальной педагогики и психологии
- Основы теории цепей
- Основы философии
- Основы экономики
- Педагогика
- Политология
- Почвоведение
- Право социального обеспечения
- Правовая статистика
- Правоведение
- Правовое обеспечение профессиональной деятельности
- Правовое регулирование профессиональной деятельности
- Правоохранительные органы
- Прикладная механика
- Программирование
- Прокурорский надзор
- Пропедевтика внутренних болезней
- Психология
- Психология и педагогика
- Психология социально-правовой деятельности
- Радиотехнические цепи и сигналы
- Римское право
- Риторика
- Русский язык
- Русский язык и культура речи
- Сетевая экономика
- Сопротивление материалов
- Социальная психология
- Социология
- Статистика
- Стратегический менеджмент
- Теоретическая механика
- Теоретические основы электротехники
- Теория автоматического управления
- Теория вероятностей и математическая статистика
- Теория государства и права
- Теория дискретных устройств автоматики и телемеханики
- Теория и история физической культуры
- Теория механизмов и машин
- Теплотехника
- Теплоэнергетика
- Техническая механика
- Технология конструкционных материалов
- Технология социальной работы
- Токсикологическая химия
- Торговое законодательство зарубежных стран
- Трудовое право
- Уголовное право
- Физика
- Физиология и биохимия растений
- Физиология и этология животных
- Физиология растений
- Физическая культура
- Философия
- Финансовый менеджмент
- Финансы и кредит
- Французский язык
- Химия
- Экологические основы природопользования
- Экологическое право
- Экология
- Эконометрика
- Экономика
- Экономика организации (предприятия)
- Экономическая теория
- Экономический анализ
- Электрические машины и электропривод
- Электротехника и электроника
- Электроэнергетика
- Эпидемиология
- Этика деловых отношений
- Юридическая психология