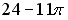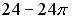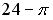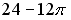Вопрос № 849019 - Математика
Мера плоского множества, изображенного на рисунке, в пространстве
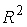равна … 
Вопрос задал(а): Анонимный пользователь, 13 Ноябрь 2020 в 15:19
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 15:19
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 15:19
Похожие вопросы
Мера плоского множества, изображенного на рисунке, в пространстве
равна … 
Мера плоского множества, изображенного на рисунке,
в пространстве
равна …
в пространстве
равна … 
Другие вопросы по предмету Математика
Мера плоского множества, изображенного на рисунке, в пространстве
равна … 
Отображение отрезка 
на отрезок 
может быть задано функцией …
на отрезок может быть задано функцией … 
Отображение интервала 
на интервал 
может быть задано функцией …
на интервал может быть задано функцией … 
Из указанных метрических пространств:
– множество всех непрерывных действительных функций, определенных на отрезке 
с расстоянием 
;
– пространство, точками которого служат всевозможные последовательности 
действительных чисел, удовлетворяющие условию 
, а расстояние определяется формулой 
;
– множество всех непрерывно дифференцируемых действительных функций, определенных на отрезке 
с расстоянием 
;
– множество упорядоченных групп из n действительных чисел 
с расстоянием 
, –
полным не является …
– множество всех непрерывных действительных функций, определенных на отрезке с расстоянием ; – пространство, точками которого служат всевозможные последовательности действительных чисел, удовлетворяющие условию , а расстояние определяется формулой ; – множество всех непрерывно дифференцируемых действительных функций, определенных на отрезке с расстоянием ; – множество упорядоченных групп из n действительных чисел с расстоянием , –полным не является …
