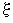Подвижный конус А катится без проскальзывания по неподвижному конусу В так что угловая скорость вращ...: ответ на тест 169175 - Теоретическая механика
Подвижный конус А катится без проскальзывания по неподвижному конусу В так, что угловая скорость вращения оси ОС вокруг оси ОС1 неподвижного конуса постоянна и равна 
с-1.
Направление вектора мгновенного углового ускорения совпадает с направлением…
с-1.Направление вектора мгновенного углового ускорения совпадает с направлением… 
Вопрос задал(а): Анонимный пользователь, 22 Декабрь 2019 в 22:11
На вопрос ответил(а): Чернышова Людмила, 22 Декабрь 2019 в 22:11
На вопрос ответил(а): Чернышова Людмила, 22 Декабрь 2019 в 22:11