Кинетическая энергия системы с двумя степенями свободы равна где и – обобщенные координаты и - о...: ответ на тест 432635 - Теоретическая механика
Кинетическая энергия системы с двумя степенями свободы равна 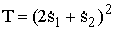 , где
, где 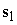 и
и 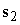 – обобщенные координаты,
– обобщенные координаты, 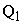 и
и 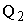 - обобщенные силы, соответствующие обобщенным координатам. Ускорение системы
- обобщенные силы, соответствующие обобщенным координатам. Ускорение системы 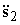 по уравнениям Лагранжа при
по уравнениям Лагранжа при 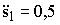 и
и 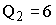 равно …
равно …
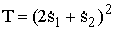 , где
, где 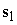 и
и 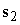 – обобщенные координаты,
– обобщенные координаты, 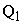 и
и 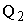 - обобщенные силы, соответствующие обобщенным координатам. Ускорение системы
- обобщенные силы, соответствующие обобщенным координатам. Ускорение системы 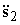 по уравнениям Лагранжа при
по уравнениям Лагранжа при 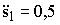 и
и 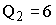 равно …
равно …
Вопрос задал(а): Анонимный пользователь, 10 Ноябрь 2020 в 13:18
На вопрос ответил(а): Анастасия Степанова, 10 Ноябрь 2020 в 13:18
На вопрос ответил(а): Анастасия Степанова, 10 Ноябрь 2020 в 13:18
