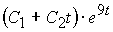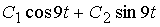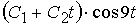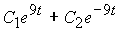Вопрос № 339910 - Теоретическая механика
Свободные колебания механической системы описываются нелинейным дифференциальным уравнением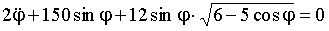 
, где 
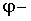обобщенная координата. Общее решение дифференциального уравнения в случае малых колебаний можно записать в ви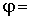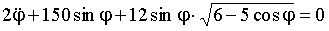де 
______
, где 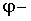обобщенная координата. Общее решение дифференциального уравнения в случае малых колебаний можно записать в виде ______ 
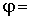Вопрос задал(а): Анонимный пользователь, 10 Ноябрь 2020 в 03:17
На вопрос ответил(а): Анастасия Степанова, 10 Ноябрь 2020 в 03:17
На вопрос ответил(а): Анастасия Степанова, 10 Ноябрь 2020 в 03:17
Похожие вопросы
Свободные колебания механической системы описываются нелинейным дифференциальным уравнением 
, где 
обобщенная координата. Общее решение дифференциального уравнения в случае малых колебаний можно записать в виде 
______
, где обобщенная координата. Общее решение дифференциального уравнения в случае малых колебаний можно записать в виде ______ 
Свободные колебания механической системы описываются нелинейным дифференциальным уравнением 
, где 
обобщенная координата. Общее решение дифференциального уравнения в случае малых колебаний можно записать в виде 
______
, где обобщенная координата. Общее решение дифференциального уравнения в случае малых колебаний можно записать в виде ______ 
Другие вопросы по предмету Теоретическая механика
Свободные колебания механической системы описываются нелинейным дифференциальным уравнением 
, где 
обобщенная координата. Общее решение дифференциального уравнения в случае малых колебаний можно записать в виде 
______
, где обобщенная координата. Общее решение дифференциального уравнения в случае малых колебаний можно записать в виде ______ 
Платформа массой 
80 кг движется по гладкой горизонтальной плоскости с постоянной скоростью 
2 м/с. По платформе движется тележка массой 
40 кг со скоростью 
3 м/c. В некоторый момент времени тележка была заторможена.
Общая скорость платформы вместе с тележкой, после остановки тележки равна … (м/с)
80 кг движется по гладкой горизонтальной плоскости с постоянной скоростью 2 м/с. По платформе движется тележка массой 40 кг со скоростью 3 м/c. В некоторый момент времени тележка была заторможена. Общая скорость платформы вместе с тележкой, после остановки тележки равна … (м/с)
1
5
3
Платформа массой 
120 кг движется по гладкой горизонтальной плоскости с постоянной скоростью 
3 м/с. По платформе движется тележка массой 
40 кг со скоростью 
4 м/c. В некоторый момент времени тележка была заторможена.
Общая скорость платформы вместе с тележкой, после остановки тележки равна … (м/с)
120 кг движется по гладкой горизонтальной плоскости с постоянной скоростью 3 м/с. По платформе движется тележка массой 40 кг со скоростью 4 м/c. В некоторый момент времени тележка была заторможена. Общая скорость платформы вместе с тележкой, после остановки тележки равна … (м/с)
7
2
3,25
4
Платформа массой 
120 кг движется по гладкой горизонтальной плоскости с постоянной скоростью 
2 м/с. По платформе движется тележка массой 
60 кг со скоростью 
2 м/c. В некоторый момент времени тележка была заторможена.
Общая скорость платформы вместе с тележкой, после остановки тележки равна … (м/с)
120 кг движется по гладкой горизонтальной плоскости с постоянной скоростью 2 м/с. По платформе движется тележка массой 60 кг со скоростью 2 м/c. В некоторый момент времени тележка была заторможена. Общая скорость платформы вместе с тележкой, после остановки тележки равна … (м/с)
4
