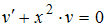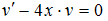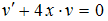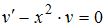Дифференциальное уравнение вида называется дифференциальным уравнением первого порядка. Для его реш...: ответ на тест 910295 - Математика
Дифференциальное уравнение вида  называется
называется
дифференциальным уравнением первого порядка. Для его решения используют подстановку: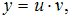 тогда
тогда 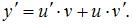 Сделав подстановку в исходное уравнение, выносят за скобки
Сделав подстановку в исходное уравнение, выносят за скобки  и выражение, стоящее в скобках, приравнивают к нулю. Из полученного уравнения находят v. Остается решить дифференциальное уравнение с разделяющимися переменными. Для дифференциального уравнения
и выражение, стоящее в скобках, приравнивают к нулю. Из полученного уравнения находят v. Остается решить дифференциальное уравнение с разделяющимися переменными. Для дифференциального уравнения 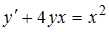 функцию
функцию 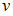 находят из уравнения …
находят из уравнения …
 называется
называетсядифференциальным уравнением первого порядка. Для его решения используют подстановку:
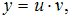 тогда
тогда 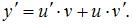 Сделав подстановку в исходное уравнение, выносят за скобки
Сделав подстановку в исходное уравнение, выносят за скобки  и выражение, стоящее в скобках, приравнивают к нулю. Из полученного уравнения находят v. Остается решить дифференциальное уравнение с разделяющимися переменными. Для дифференциального уравнения
и выражение, стоящее в скобках, приравнивают к нулю. Из полученного уравнения находят v. Остается решить дифференциальное уравнение с разделяющимися переменными. Для дифференциального уравнения 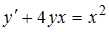 функцию
функцию 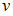 находят из уравнения …
находят из уравнения …
Вопрос задал(а): Анонимный пользователь, 13 Ноябрь 2020 в 16:09
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 16:09
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 16:09