Оценку параметров точно идентифицируемой системы эконометрических уравнений вида можно рассчитать ...: ответ на тест 90289 - Эконометрика
Оценку параметров точно идентифицируемой системы эконометрических уравнений вида

можно рассчитать с помощью косвенного метода наименьших квадратов. Определите правильную последовательность действий.

можно рассчитать с помощью косвенного метода наименьших квадратов. Определите правильную последовательность действий.
Варианты ответов
- запишем систему с найденными значениями параметров b12; b21; а11; а22
-
при помощи обычного МНК оценим параметры
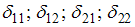
-
преобразуем структурную форму модели в приведенную форму модели вида

- на основе преобразований рассчитаем значения параметров структурной формы модели b12; b21; а11; а22
Правильный ответ
Вопрос задал(а): Анонимный пользователь, 08 Февраль 2016 в 13:00
На вопрос ответил(а): Чернышова Людмила, 08 Февраль 2016 в 13:00
На вопрос ответил(а): Чернышова Людмила, 08 Февраль 2016 в 13:00
