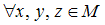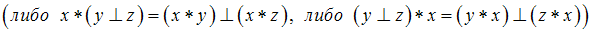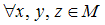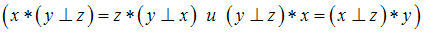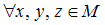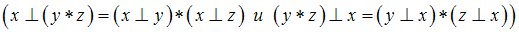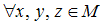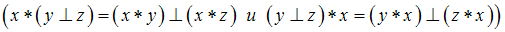Вопрос № 146956 - Математика
На множестве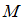 
определены бинарные алгебраические операции, обозначенные символами 
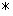и 
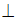, тогда операция 
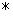дистрибутивна относительно операции 
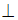, если …
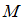определены бинарные алгебраические операции, обозначенные символам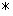и и 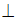, тогда операция 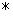дистрибутивна относительно операции 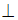, если … 
Вопрос задал(а): Анонимный пользователь, 14 Май 2017 в 15:01
На вопрос ответил(а): Бунакова Мария, 14 Май 2017 в 15:02
На вопрос ответил(а): Бунакова Мария, 14 Май 2017 в 15:02
Похожие вопросы
Известно, что алгебраическая система 
является группой, причём 
, а бинарная операция 
, определяется таблицей
.
Единичным элементом группы относительно бинарной операции является элемент
.
Тогда множество
относительно операции 
…
является группой, причём , а бинарная операция , определяется таблицей.Единичным элементом группы относительно бинарной операции является элемент
.Тогда множество
относительно операции …
является некоммутативным моноидом
не является алгебраической подсистемой группы 
является некоммутативной полугруппой
является абелевой подгруппой
На множестве 
определены бинарные алгебраические операции, обозначенные символами 
и 
, тогда операция 
дистрибутивна относительно операции 
, если …
определены бинарные алгебраические операции, обозначенные символами и , тогда операция дистрибутивна относительно операции , если … 
Другие вопросы по предмету Математика
Разложение в ряд Маклорена функции 
имеет вид:
.
Тогда разложением в ряд Маклорена функции
является …
имеет вид:.Тогда разложением в ряд Маклорена функции
является … 
На множестве натуральных чисел N определены операции …
Характеристикой поля не может быть число …
Дискретная случайная величина 
принимает два возможных значения: 
с вероятностью 0,6 и 
с вероятностью 
. Если математическое ожидание 
, тогда 
равно …
принимает два возможных значения: с вероятностью 0,6 и с вероятностью . Если математическое ожидание , тогда равно …
2,5
0,8
0,4
2