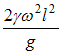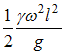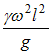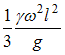Стержень ВС длиной l площадью поперечного сечения А равномерно вращается с постоянной угловой скоро...: ответ на тест 883073 - Сопротивление материалов
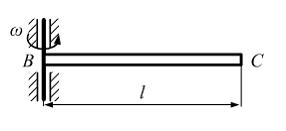
Стержень ВС длиной l, площадью поперечного сечения А равномерно вращается с постоянной угловой скоростью
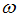 вокруг вертикальной оси. Удельный вес материала
вокруг вертикальной оси. Удельный вес материала 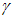 (вес единицы объема) задан. Значение максимального нормального напряжения в стержне равно …
(вес единицы объема) задан. Значение максимального нормального напряжения в стержне равно …
Вопрос задал(а): Анонимный пользователь, 13 Ноябрь 2020 в 15:34
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 15:34
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 15:34