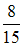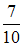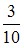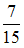В первой урне 7 белых и 3 черных шара. Во второй урне 4 белых и 6 черных шаров. В третьей урне 3 бел...: ответ на тест 1085455 - Математика
В первой урне 7 белых и 3 черных шара. Во второй урне 4 белых и 6 черных шаров. В третьей урне 3 белых и 7 черных шаров. Из наудачу взятой урны вынули один шар. Тогда вероятность того, что этот шар черный, равна …
Вопрос задал(а): Анонимный пользователь, 13 Ноябрь 2020 в 19:26
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 19:26
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 19:26