Из вершины острого угла проведены перпендикуляры к прямым содержащим стороны ромба которым не принад...: ответ на тест 174712 - Русский язык
Из вершины острого угла проведены перпендикуляры к прямым, содержащим стороны ромба, которым не принадлежит эта вершина. Длина каждого перпендикуляра равна 3, а расстояние между их основаниями равно 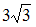 . Вычислите длину наибольшей диагонали ромба.
. Вычислите длину наибольшей диагонали ромба.
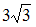 . Вычислите длину наибольшей диагонали ромба.
. Вычислите длину наибольшей диагонали ромба.
Вопрос задал(а): Анонимный пользователь, 10 Ноябрь 2020 в 00:05
На вопрос ответил(а): Анастасия Степанова, 10 Ноябрь 2020 в 00:05
На вопрос ответил(а): Анастасия Степанова, 10 Ноябрь 2020 в 00:05
