Если последовательные значения функции являющейся решением задачи Коши для дифференциального уравнен...: ответ на тест 405205 - Математика
Если последовательные значения функции, являющейся решением задачи Коши для дифференциального уравнения 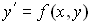 с начальными условиями
с начальными условиями 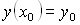 ,
, 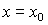 , находятся по методу Эйлера
, находятся по методу Эйлера 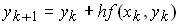 , то
, то 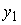 , определяемое уравнением
, определяемое уравнением 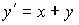 , при
, при 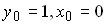 и шаге
и шаге 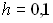 , равно …
, равно …
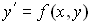 с начальными условиями
с начальными условиями 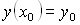 ,
, 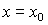 , находятся по методу Эйлера
, находятся по методу Эйлера 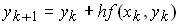 , то
, то 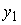 , определяемое уравнением
, определяемое уравнением 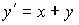 , при
, при 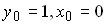 и шаге
и шаге 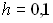 , равно …
, равно …
Вопрос задал(а): Анонимный пользователь, 10 Ноябрь 2020 в 13:06
На вопрос ответил(а): Анастасия Степанова, 10 Ноябрь 2020 в 13:06
На вопрос ответил(а): Анастасия Степанова, 10 Ноябрь 2020 в 13:06
