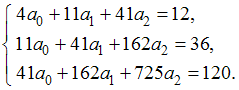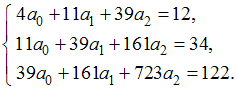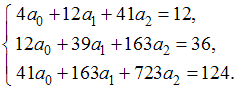Функция представлена таблицей Эта функция аппроксимируется квадратичной зависимостью методом наим...: ответ на тест 860295 - Математика

Функция 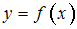 представлена таблицей

Эта функция аппроксимируется квадратичной зависимостью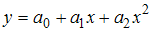  методом наименьших квадратов.
Тогда коэффициенты аппроксимирующей функции определяются системой уравнений …

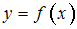Функция  представлена таблицей

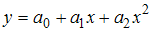Аппроксимирующей линейной функцией, найденной методом наименьших квадратов, для заданной функции служит …

Интеграл вычисляется при помощи разложения подынтегральной функции в степенной ряд. Тогда его значение с точностью 0,001 равно …

Таблица

представляет значения функции  в некоторых точках.
Используя формулы, основанные на интерполяционном полиноме Лагранжа, вычисляются, с тремя знаками после запятой, значения производной  заданной функции в точках , , .
Тогда значения  в указанных точках соответственно равны …

Функция  представлена таблицей

Известно, что на отрезке  максимальное значение производной третьего порядка  равно 12. В точке  вычислено значение производной  на основе интерполяционного полинома Лагранжа 2-й степени.
Тогда погрешность (округлённая до двух знаков после запятой) не превышает значения …

Функция  представлена таблицей


Значение интеграла  вычисляется методом Симпсона, а точность (погрешность) оценивается по методу Рунге – Ромберга. Погрешностями округлений пренебрегают.
Тогда значения интеграла и погрешности соответственно равны …