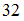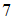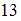Вопрос № 860254 - Математика
Символом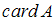 
обозначим число элементов множества 
.
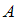Известно, что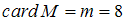
, 
, 
,
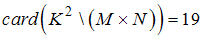, где 
.
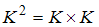Тогда число элементов множества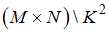
равно …
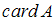обозначим число элементов множества 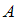.Известно, что
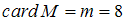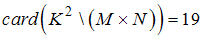, , ,, где 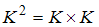.Тогда число элементов множества
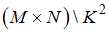равно … 
Вопрос задал(а): Анонимный пользователь, 13 Ноябрь 2020 в 15:21
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 15:21
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 15:21
Похожие вопросы
Символом 
обозначим число элементов множества 
.
Известно, что
, 
, 
,
, где 
.
Тогда число элементов множества
равно …
обозначим число элементов множества .Известно, что
, , ,, где .Тогда число элементов множества
равно … 
Пусть 
, причём для любых индексов 
, т.е. множества 
, 
и 
образуют разбиение множества 
на подмножества.
Известно, что
(
– число элементов множества 
), 
, 
, 
.
Тогда число вариантов разбиения множества
на подмножества указанным выше способом равно …
, причём для любых индексов , т.е. множества , и образуют разбиение множества на подмножества.Известно, что
( – число элементов множества ), , , .Тогда число вариантов разбиения множества
на подмножества указанным выше способом равно … 
Другие вопросы по предмету Математика
Пусть на множестве 
задано бинарное отношение, которое описано множеством 
, причём
.
Тогда матрицей этого бинарного отношения является …
задано бинарное отношение, которое описано множеством , причём.Тогда матрицей этого бинарного отношения является …
Отображение 
, где 
– множество действительных чисел, определяется соотношением 
(или 
, где 
).
Тогда прообразом множества
при отображении 
служит множество …
, где – множество действительных чисел, определяется соотношением (или , где ).Тогда прообразом множества
при отображении служит множество … 
, 
– множество целых чисел
Даны множества 
и 
и отображение 
, представленное в виде
.
Пусть
.
Тогда прообраз
множества 
есть множество …
и и отображение , представленное в виде.Пусть
. Тогда прообраз
множества есть множество … 
Даны:
1) множества
и 
;
2) отображения
и 
, причём отображения определяются следующим образом:
и
.
Тогда композиция
(сначала 
, а потом 
) отображений 
и 
есть отображение …
1) множества
и ;2) отображения
и , причём отображения определяются следующим образом:и
.Тогда композиция
(сначала , а потом ) отображений и есть отображение … 
