Вопрос № 852581 - Математика
Пусть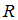 
– множество всех действительных чисел, а 
, 
, 
, 
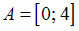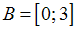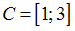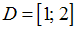– его подмножества.
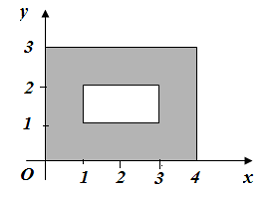
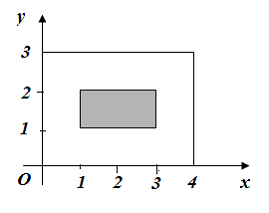
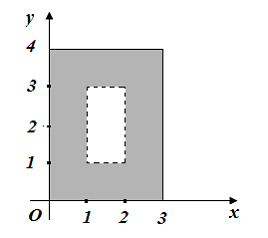
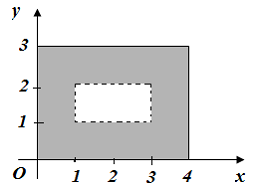
Тогда геометрической интерпретацией множества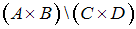
может служить …
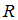– множество всех действительных чисел, а 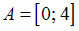, , 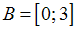, 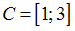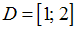– его подмножества.Тогда геометрической интерпретацией множества
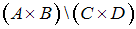может служить … 
Вопрос задал(а): Анонимный пользователь, 13 Ноябрь 2020 в 15:19
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 15:19
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 15:19
Похожие вопросы
Пусть 
– множество всех действительных чисел, а 
, 
, 
, 
– его подмножества.
Тогда геометрической интерпретацией множества
может служить …
– множество всех действительных чисел, а , , , – его подмножества.Тогда геометрической интерпретацией множества
может служить … 
Дано множество 
и его подмножества 
, 
и 
, причём
, 
, 
.
Пусть
и 
– булеан множества 
, т.е. множество всех подмножеств множества 
.
Тогда истинно утверждение:
и его подмножества , и , причём , , .Пусть
и – булеан множества , т.е. множество всех подмножеств множества .Тогда истинно утверждение:
Другие вопросы по предмету Математика
На множестве 
введено бинарное отношение, обозначенное буквой 
(если элементы 
и элемент 
находится в отношении 
с элементом 
, то записываем 
).
Это отношение определяется так:
, если 
делится (нацело) на число 
.
Пусть множество
. Тогда множество 
есть множество …
введено бинарное отношение, обозначенное буквой (если элементы и элемент находится в отношении с элементом , то записываем ).Это отношение определяется так:
, если делится (нацело) на число .Пусть множество
. Тогда множество есть множество … 
Пусть на множестве 
задано бинарное отношение, которое описано множеством 
, причём
.
Тогда матрицей этого бинарного отношения является …
задано бинарное отношение, которое описано множеством , причём.Тогда матрицей этого бинарного отношения является …
Пусть 
– множество целых чисел, на котором определены указанные бинарные отношения.
Тогда отношением эквивалентности является отношение …
– множество целых чисел, на котором определены указанные бинарные отношения.Тогда отношением эквивалентности является отношение …
: 
, если числа 
и число 
делит (нацело) число 
. 
: 
, если числа 
и справедливо неравенство 
. 
: 
, если числа 
и число 
является нечётным числом. 
: 
, если числа 
и число 
делится (нацело) на число 
.
Даны множества 
и 
и отображение 
, представленное в виде
.
Пусть
– множество простых чисел множества 
, тогда образ 
есть …
и и отображение , представленное в виде.Пусть
– множество простых чисел множества , тогда образ есть … 
