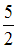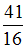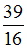Функция представлена таблицей Для вычисления значения функции в точке используется интерполяцион...: ответ на тест 860291 - Математика
Функция 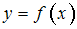 представлена таблицей
представлена таблицей
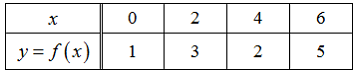
Для вычисления значения функции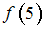 в точке
в точке  используется интерполяционный полином Ньютона
используется интерполяционный полином Ньютона 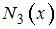 (интерполяция вперёд).
(интерполяция вперёд).
Тогда равно …
равно …
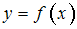 представлена таблицей
представлена таблицей
Для вычисления значения функции
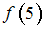 в точке
в точке  используется интерполяционный полином Ньютона
используется интерполяционный полином Ньютона 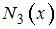 (интерполяция вперёд).
(интерполяция вперёд).Тогда
 равно …
равно …
Вопрос задал(а): Анонимный пользователь, 13 Ноябрь 2020 в 15:22
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 15:22
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 15:22