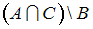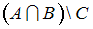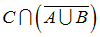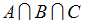Вопрос № 852576 - Математика
На рисунке показаны следующие множества: основное (универсальное) множество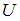 
и его подмножества 
, 
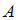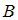и 
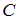(соответствующие прямоугольные области на плоскости).
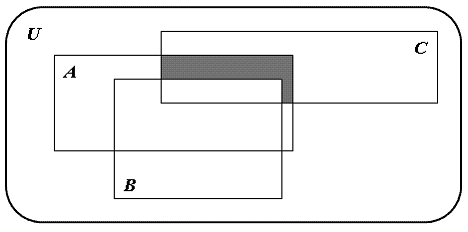
Тогда закрашенное подмножество есть …
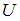и его подмножества 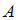, 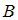и 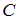(соответствующие прямоугольные области на плоскости).Тогда закрашенное подмножество есть …
Вопрос задал(а): Анонимный пользователь, 13 Ноябрь 2020 в 15:19
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 15:19
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 15:19
Похожие вопросы
На рисунке показаны следующие множества: основное (универсальное) множество 
и его подмножества 
, 
и 
(соответствующие прямоугольные области на плоскости).
Тогда закрашенное подмножество есть …
и его подмножества , и (соответствующие прямоугольные области на плоскости).Тогда закрашенное подмножество есть …
Пусть 
– произвольное множество (универсальное), 
– произвольное подмножество, 
– дополнения множества 
до множества 
(разность множеств 
и 
).
Тогда доказательство тождества
образует последовательность приведённых утверждений …
– произвольное множество (универсальное), – произвольное подмножество, – дополнения множества до множества (разность множеств и ).Тогда доказательство тождества
образует последовательность приведённых утверждений … 
- произвольный элемент множества 
(кратко:
).
Соотношение 
в силу определения операции пересечения множеств равносильно соотношению: 
и 
(кратко:
).
в силу определения операции пересечения множеств равносильно соотношению: и (кратко:
).
Соотношения 
и 
равносильны, это следует из определения операции дополнения
(кратко:
).
и равносильны, это следует из определения операции дополнения(кратко:
).
Соотношение 
и 
есть противоречие, а поэтому 
(кратко:
).
и есть противоречие, а поэтому (кратко:
). Другие вопросы по предмету Математика
Дано множество
.
Пусть
– булеан множества 
, т.е. множество всех подмножеств множества 
.
Тогда истинным будет соотношение …
.Пусть
– булеан множества , т.е. множество всех подмножеств множества .Тогда истинным будет соотношение …
Для множества 
построено множество 
, т.е. булеан множества 
(множество всех подмножеств множества 
). Из этого булеана удалили пустое множество 
и все одноэлементные множества. Полученное в результате множество обозначили символом 
и построили его булеан 
.
Тогда число элементов множества
равно …
построено множество , т.е. булеан множества (множество всех подмножеств множества ). Из этого булеана удалили пустое множество и все одноэлементные множества. Полученное в результате множество обозначили символом и построили его булеан .Тогда число элементов множества
равно … 
Декартово произведение числовых множеств 
, 
и 
определяется как …
, и определяется как … 
Если количество элементов множества А равно n, количество элементов множества В равно m, тогда количество элементов в декартовом произведении 
равно …
равно … 
2∙( m + n )
