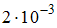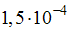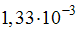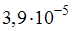Для функции известны её значения в узлах . Требуется вычислить значение этой функции в точке . Д...: ответ на тест 860289 - Математика
Для функции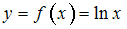 
известны её значения в узлах 
, 
, 
, 
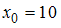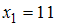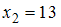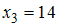. Требуется вычислить значение этой функции в точке 
.
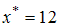Для вычисления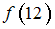
используется интерполяционный полином Лагранжа 
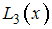3-й степени. Погрешностями округлений пренебрегают.
Тогда величина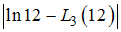
не превышает …
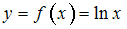известны её значения в узлах 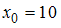, , 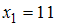, 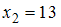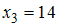. Требуется вычислить значение этой функции в точке 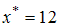.Для вычисления
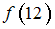используется интерполяционный полином Лагранжа 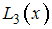3-й степени. Погрешностями округлений пренебрегают.Тогда величина
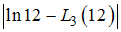не превышает … 
Вопрос задал(а): Анонимный пользователь, 13 Ноябрь 2020 в 15:22
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 15:22
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 15:22